
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,

 .
.

(Ⅰ)求证:CD⊥平面ADD1A1;
(Ⅱ)若直线AA1与平面AB1C所成角的正弦值为 ,求k的值.
,求k的值.
(Ⅰ)见解析(Ⅱ)1
【解析】
试题分析:(Ⅰ)取CD的中点为E,连结BE,则ADEB为平行四边形,所以AD BE=4k,所以BC2=BE2+EC2,所以BE⊥DC,所以AD与BC垂直,AA1⊥面ABCD,所以AA1⊥CD,所以CD垂直面AA1D1D;(Ⅱ)以D为原点,DA,DC,DD1为
BE=4k,所以BC2=BE2+EC2,所以BE⊥DC,所以AD与BC垂直,AA1⊥面ABCD,所以AA1⊥CD,所以CD垂直面AA1D1D;(Ⅱ)以D为原点,DA,DC,DD1为 轴,建立空间直角坐标系,写出A、A1,B1,C的坐标,求出面AB1C的一个法向量,算出向量
轴,建立空间直角坐标系,写出A、A1,B1,C的坐标,求出面AB1C的一个法向量,算出向量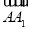 坐标,计算出这两个向量的夹角,再利用向量夹角与线面角关系,列出关于k的方程,若能解出k值..
坐标,计算出这两个向量的夹角,再利用向量夹角与线面角关系,列出关于k的方程,若能解出k值..
试题解析:(Ⅰ)取CD的中点E,连结BE.
∵AB∥DE,AB DE
DE 3k,∴四边形ABED为平行四边形, 2分
3k,∴四边形ABED为平行四边形, 2分
∴BE∥AD且BE AD
AD 4k.
4k.
在△BCE中,∵BE 4k,CE
4k,CE 3k,BC
3k,BC 5k,∴BE2+CE2
5k,∴BE2+CE2 BC2,
BC2,
∴∠BEC 90°,即BE⊥CD,
90°,即BE⊥CD,
又∵BE∥AD,∴CD⊥AD. 4分
∵AA1⊥平面ABCD,CD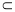 平面ABCD,
平面ABCD,
∴AA1⊥CD.又AA1∩AD A,
A,
 ADD1A1. 6分
ADD1A1. 6分
(Ⅱ)以D为原点, ,
, ,
,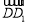 的方向为x,y,z轴的正方向建立如图所示的空间直角坐标系,
的方向为x,y,z轴的正方向建立如图所示的空间直角坐标系,
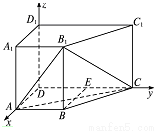
则
所以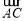
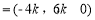 ,
,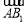
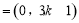 ,
,
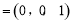 .
.
设平面AB1C的法向量n (x,y,z),
(x,y,z),
则由 得
得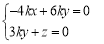
取y 2,得
2,得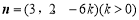 . 9分
. 9分
设AA1与平面AB1C所成角为θ,则
sin θ |cos〈
|cos〈 ,n〉|
,n〉|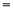
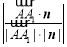
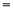
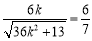 ,
,
解得k 1,故所求k的值为1. 12分
1,故所求k的值为1. 12分
考点:面面垂直的性质,线面垂直的判定,线面角的计算,推理论证能力,运算求解能力,空间想象能力


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届河北省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知函数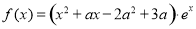 ,其中
,其中 .
.
(1)是否存在实数 ,使得函数
,使得函数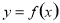 在
在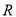 上单调递增?若存在,求出的
上单调递增?若存在,求出的 值或取值范围;否则,请说明理由.
值或取值范围;否则,请说明理由.
(2)若a<0,且函数y=f(x)的极小值为 ,求函数的极大值。
,求函数的极大值。
查看答案和解析>>
科目:高中数学 来源:2015届河北省“五个一名校联盟”高三教学质量监测一理科数学试卷(解析版) 题型:填空题
已知函数 的图像为曲线C,若曲线C存在与直线
的图像为曲线C,若曲线C存在与直线 垂直的切线,则实数m的取值范围是_____________.
垂直的切线,则实数m的取值范围是_____________.
查看答案和解析>>
科目:高中数学 来源:2015届河北省“五个一名校联盟”高三教学质量监测一理科数学试卷(解析版) 题型:选择题
学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有 ( )
A.36种 B.30种 C.24种 D.6种
查看答案和解析>>
科目:高中数学 来源:2015届河北省“五个一名校联盟”高三教学质量监测一文科数学试卷(解析版) 题型:填空题
已知函数 的图像为曲线C,若曲线C存在与直线
的图像为曲线C,若曲线C存在与直线 垂直的切线,则实数
垂直的切线,则实数 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:高中数学 来源:2015届河北唐山一中高二下学期期末考试文科数学试卷(解析版) 题型:解答题
在直角坐标系xOy中,直线l的方程为x﹣y+4=0,曲线C的参数方程为 (α为参数)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,
(α为参数)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4, ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com