
 ,则一定有
,则一定有 ;
;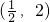 ;
; 与
与 的夹角为锐角的充要条件是
的夹角为锐角的充要条件是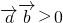 .
. 、
、 为非零向量;②显然存在x=y=0满足题意;③将定点代入验证即可;④利用圆的一般方程的特点即可判断;⑤
为非零向量;②显然存在x=y=0满足题意;③将定点代入验证即可;④利用圆的一般方程的特点即可判断;⑤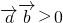 时,两向量可能共线
时,两向量可能共线 ,则
,则 可能为
可能为 ,而
,而 方向不定,故
方向不定,故 、
、 不一定垂直,故①假;
不一定垂直,故①假;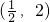 代入函数解析式,显然正确,故③正确;
代入函数解析式,显然正确,故③正确; 与
与 的夹角为锐角的充要条件是
的夹角为锐角的充要条件是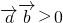 且
且 、
、 不共线,故⑤错误;
不共线,故⑤错误;

科目:高中数学 来源: 题型:
| x2 |
| 5-m |
| y2 |
| m+3 |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 5-m |
| y2 |
| m+3 |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| x2 |
| 25 |
| y2 |
| 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com