
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的方程是
的方程是![]() (
(![]() ,
,![]() ).
).
(1)当![]() ,
,![]() 时,求曲线
时,求曲线![]() 围成的区域的面积;
围成的区域的面积;
(2)若直线![]() :
:![]() 与曲线
与曲线![]() 交于
交于![]() 轴上方的两点
轴上方的两点![]() ,
,![]() ,且
,且![]() ,求点
,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品所得利润分别为![]() 和
和![]() (万元),它们与投入资金
(万元),它们与投入资金![]() (万元)的关系有如下公式:
(万元)的关系有如下公式:![]() ,
,![]() ,今将200万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于25万元.
,今将200万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于25万元.
(Ⅰ)设对乙种产品投入资金![]() (万元),求总利润
(万元),求总利润![]() (万元)关于
(万元)关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(Ⅱ)如何分配投入资金,才能使总利润最大,并求出最大总利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2009四川卷文)设矩形的长为![]() ,宽为
,宽为![]() ,其比满足
,其比满足![]() ∶
∶![]() =
=![]() ,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是
A. 甲批次的总体平均数与标准值更接近
B. 乙批次的总体平均数与标准值更接近
C. 两个批次总体平均数与标准值接近程度相同
D. 两个批次总体平均数与标准值接近程度不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有4个人去参加娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1)求这4个人中恰有2人去参加甲游戏的概率;
(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列与数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
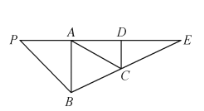
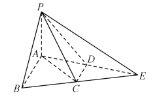
【题目】如图,在![]() 中,
中,![]() ,D是AE的中点,C是线段BE上的一点,且
,D是AE的中点,C是线段BE上的一点,且![]() ,
,![]() ,将
,将![]() 沿AB折起使得二面角
沿AB折起使得二面角![]() 是直二面角.
是直二面角.
(l)求证:CD平面PAB;
(2)求直线PE与平面PCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,中心在坐标原点,抛物线
轴上,中心在坐标原点,抛物线![]() 的焦点在
的焦点在![]() 轴上,顶点在坐标原点,在
轴上,顶点在坐标原点,在![]() 、
、![]() 上各取两个点,将其坐标记录于表格中:
上各取两个点,将其坐标记录于表格中:
|
|
|
|
|
|
|
|
|
|
(1)求![]() 、
、![]() 的标准方程;
的标准方程;
(2)已知定点![]() ,
,![]() 为抛物线
为抛物线![]() 上的一点,其横坐标为
上的一点,其横坐标为![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线交椭圆
处的切线交椭圆![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 面积.
面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程ay=b2x2+c中的a,b,c∈{﹣3,﹣2,0,1,2,3},且a,b,c互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有( )
A.60条
B.62条
C.71条
D.80条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 的线性回归直线方程为
的线性回归直线方程为![]() ,且
,且![]() ,
,![]() 之间的一组相关数据如下表所示,则下列说法错误的为
之间的一组相关数据如下表所示,则下列说法错误的为

A.变量![]() ,
,![]() 之间呈现正相关关系B.可以预测,当
之间呈现正相关关系B.可以预测,当![]() 时,
时,![]()
C.![]() D.由表格数据可知,该回归直线必过点
D.由表格数据可知,该回归直线必过点![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com