
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的值;
的值;
(2)若![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2) a≥-1
(2) a≥-1
【解析】试题分析:(1)求出![]() 通过①若a≥-1,判断单调性求解最值;②若a≤-e,③若-e<a<-1,求出函数的最值,即可得到a的值;
通过①若a≥-1,判断单调性求解最值;②若a≤-e,③若-e<a<-1,求出函数的最值,即可得到a的值;
(2)化简表达式为:a>![]() .令g(x)=
.令g(x)= ![]() ,求出h(x)=g′(x)=1+lnx-3x2,求出导数,判断函数的单调性,求出函数的最值,即可推出结果.
,求出h(x)=g′(x)=1+lnx-3x2,求出导数,判断函数的单调性,求出函数的最值,即可推出结果.
试题解析:
(1) f′(x)=![]() .
.
①若a≥-1,则x+a≥0,即f′(x)≥0在[1,e]上恒成立,
此时f(x)在[1,e]上为增函数,∴f(x)min=f(1)=-a=![]() ,∴a=-
,∴a=-![]() (舍去).
(舍去).
②若a≤-e,则x+a≤0,即f′(x)≤0在[1,e]上恒成立,
此时f(x)在[1,e]上为减函数,∴f(x)min=f(e)=1-![]() =
=![]() ,∴a=-
,∴a=-![]() (舍去).
(舍去).
③若-e<a<-1,令f′(x)=0得x=-a,
当1<x<-a时,f′(x)<0,∴f(x)在(1,-a)上为减函数;当-a<x<e时,f′(x)>0,∴f(x)在(-a,e)上为增函数,
∴f(x)min=f(-a)=ln(-a)+1=![]() ,∴a=-
,∴a=-![]() .综上所述,a=-
.综上所述,a=-![]() .
.
(2)∵f(x)<x2,∴ln x-![]() <x2.又x>0,∴a>xln x-x3.令g(x)=xln x-x3,h(x)=g′(x)=1+ln x-3x2,h′(x)=
<x2.又x>0,∴a>xln x-x3.令g(x)=xln x-x3,h(x)=g′(x)=1+ln x-3x2,h′(x)=![]() -6x=
-6x=![]() .∵x∈(1,+∞)时,h′(x)<0,∴h(x)在(1,+∞)上是减函数.
.∵x∈(1,+∞)时,h′(x)<0,∴h(x)在(1,+∞)上是减函数.
∴h(x)<h(1)=-2<0,即g′(x)<0,∴g(x)在(1,+∞)上也是减函数.g(x)<g(1)=-1,
∴当a≥-1时,f(x)<x2在(1,+∞)上恒成立.


科目:高中数学 来源: 题型:
【题目】【2018贵州遵义市高三上学期第二次联考】设抛物线![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,抛物线的焦点为
,抛物线的焦点为![]() ,以
,以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆与抛物线的一个交点为
的椭圆与抛物线的一个交点为 ;自
;自![]() 引直线交抛物线于
引直线交抛物线于![]() 两个不同的点,设
两个不同的点,设![]() .
.
(Ⅰ)求抛物线的方程和椭圆的方程;
(Ⅱ)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】无穷数列![]() 满足:
满足: ![]() 为正整数,且对任意正整数
为正整数,且对任意正整数![]() ,
, ![]() 为前
为前![]() 项
项![]() ,
, ![]() ,
, ![]() ,
, ![]() 中等于
中等于![]() 的项的个数.
的项的个数.
(Ⅰ)若![]() ,请写出数列
,请写出数列![]() 的前7项;
的前7项;
(Ⅱ)求证:对于任意正整数![]() ,必存在
,必存在![]() ,使得
,使得![]() ;
;
(Ⅲ)求证:“![]() ”是“存在
”是“存在![]() ,当
,当![]() 时,恒有
时,恒有![]()
![]() 成立”的充要条件。
成立”的充要条件。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据中国日报网报道:2017年11月13日,TOP500发布的最新一期全球超级计算机500强榜单显示,中国超算在前五名中占据两席.其中超算全球第一“神威·太湖之光”完全使用了国产品牌处理器.为了了解国产品牌处理器打开文件的速度,某调查公司对两种国产品牌处理器进行了12次测试,结果如下:(数值越小,速度越快,单位是MIPS)

(Ⅰ)从品牌![]() 的12次测试中,随机抽取一次,求测试结果小于7的概率;
的12次测试中,随机抽取一次,求测试结果小于7的概率;
(Ⅱ)从12次测试中,随机抽取三次,记![]() 为品牌
为品牌![]() 的测试结果大于品牌
的测试结果大于品牌![]() 的测试结果的次数,求
的测试结果的次数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(Ⅲ)经过了解,前6次测试是打开含有文字与表格的文件,后6次测试时打开含有文字与图片的文件.请你依据表中数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 是曲线
是曲线![]() 上的一动点,以坐标原点为极点,
上的一动点,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的方程为
的方程为![]()
![]() .
.
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹的极坐标方程;
的轨迹的极坐标方程;
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
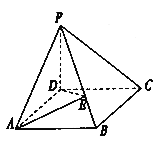
【题目】如图在棱锥![]() 中,
中, ![]() 为矩形,
为矩形, ![]() 面
面![]() ,
, ![]() ,
, ![]() 与面
与面![]() 成
成![]() 角,
角, ![]() 与面
与面![]() 成
成![]() 角.
角.
(1)在![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 面
面![]() ,若存在确定
,若存在确定![]() 点位置,若不存在,请说明理由;
点位置,若不存在,请说明理由;
(2)当![]() 为
为![]() 中点时,求二面角
中点时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com