
探究:把参数方程化为普通方程的基本思路是消去参数,常用的消参方法有代入消参法、加减消参法、恒等式(三角的或代数的)消参法;
把普通方程化为参数方程的基本思路是引入参数,是消参的逆过程,即选定合适的参数t,先确定一个关系x=f(t)〔或y=φ(t)〕,再代入普通方程F(x,y)=0,求得另一关系y=φ(t)〔或x=f(t)〕.一般地,常选择的参数有角、有向线段的数量、斜率,某一点的横坐标(或纵坐标).
在将曲线的参数方程化为普通方程时,不仅仅是要把其中的参数消去,还要注意其中的x、y的取值范围,如 (t为参数),通过消参数得到方程y2=-(x-1),而事实上由x=cos2t可知0≤x≤1,而由y2=-(x-1)可知其中x≤1,显然两个范围不同,即两个方程所表示的曲线就不是同一条曲线,可以说y2=-(x-1)就不是
(t为参数),通过消参数得到方程y2=-(x-1),而事实上由x=cos2t可知0≤x≤1,而由y2=-(x-1)可知其中x≤1,显然两个范围不同,即两个方程所表示的曲线就不是同一条曲线,可以说y2=-(x-1)就不是 的普通方程.故在消去参数的过程中一定要注意普通方程与参数方程的等价性,即它们二者要表示同一曲线.
的普通方程.故在消去参数的过程中一定要注意普通方程与参数方程的等价性,即它们二者要表示同一曲线.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
|
|
| π |
| 4 |
3
| ||
| 2 |
| a2 |
| b |
| b2 |
| a |
| (1-x)2 |
| x |
| x2 |
| 1-x |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
查看答案和解析>>
科目:高中数学 来源:2013届山西省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知圆方程为 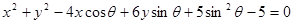
(1)求圆心轨迹的参数方程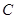 和普通方程;
和普通方程;
(2)点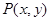 是(1)中曲线
是(1)中曲线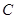 上的动点,求
上的动点,求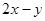 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com