【题目】已知函数
．
（1）求函数
的单调区间；
（2）若当
时，函数
的图象恒在函数
的图象的上方，求实数
的取值范围．
【答案】（1）
在
上单调递减，在
上单调递增；（2）
.
【解析】
试题分析：（1）对函数
进行求导，
，当
时，
；当
时，
，得单调区间；（2）将函数
的图象恒在函数
的图象的上方转化为不等式
在
上恒成立．
试题解析：（1）因为
，所以，
令
，得
，
因为当时，；当时，，
所以函数在上单调递减，在上单调递增．
（2）由当
时，函数的图象恒在函数的图象的上方，
可得不等式在上恒成立．
设
，
则
①当
时，因为
在
上恒成立，所以
在
上是增函数，又因为
，所以当
时，总有
，不符合题意．
②当
时，因为
在上恒成立，所以在上是减函数，又因为，所以当时，总有
，符合题意．
③当
时，令
，解得
，
在
上是增函数，在
上是减函数，又因为
，所以当
时，总有，不符合题意.
综上，实数
的取值范围为．
科目：高中数学 来源： 题型：
【题目】已知椭圆
短轴的一个端点与其两个焦点构成面积为3的直角三角形.
（1）求椭圆
的方程；
（2）过圆
上任意一点
作圆
的切线
， 
与椭圆
交于
两点，以
为直径的圆是否过定点，如过，求出该定点；不过说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商店计划每天购进某商品若干件，商店每销售一件该商品可获利润60元，若供大于求，剩余商品全部退回，但每件商品亏损10元；若供不应求，则从外部调剂，此时每件调剂商品可获利40元.
（1）若商品一天购进该商品10件，求当天的利润
（单位：元）关于当天需求量
（单位：件，
）的函数解析式；
（2）商店记录了50天该商品的日需求量
（单位：件，
），整理得下表：
若商店一天购进10件该商品，以50天记录的各需求量的频率作为各需求量发生的概率，求当天的利润在区间
内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两同学在高考前各做了5次立定跳远测试，测得甲的成绩如下(单位：米)：2.20，2.30，2.30，2.40，2.30，若甲、乙两人的平均成绩相同，乙的成绩的方差是0.005，那么甲、乙两人成绩较稳定的是________．
查看答案和解析>>
科目：高中数学 来源： 题型：
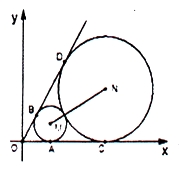
【题目】如图，已知圆心坐标为
的圆
与
轴及直线
分别相切于
、
两点，另一圆
与圆
外切，且与
轴及直线分别相切于
、
两点．
（1）求圆和圆
的方程；
（2）过点
作直线
的平行线
，求直线
被圆
截得的弦的长度．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知α、β是不同的平面，l、m、n是不同的直线，P为空间中一点．若α∩β＝l，mα、nβ、m∩n＝P，则点P与直线l的位置关系用符号表示为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
