
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:

经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的概率);①
表示相应事件的概率);①![]() ;②
;②![]() ;③
;③![]() ,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备
,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
(ⅰ)若从设备![]() 的生产流水线上随意抽取
的生产流水线上随意抽取![]() 件零件,求恰有一件次品的概率;
件零件,求恰有一件次品的概率;
(ⅱ)若从样本中随意抽取![]() 件零件,计算其中次品个数
件零件,计算其中次品个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【答案】(1)该设备![]() 的性能为丙级别;(2)(ⅰ)
的性能为丙级别;(2)(ⅰ)![]() ;(ⅱ)分布列见解析,
;(ⅱ)分布列见解析,![]() .
.
【解析】
(1)利用条件,根据表格中的数据验证随机变量![]() 是否满足①②③中的不等式,即可得出结论;
是否满足①②③中的不等式,即可得出结论;
(2)(i)计算出从设备![]() 的生产流水线上任取一件为次品的概率,然后利用独立重复试验的概率公式可计算出结果;
的生产流水线上任取一件为次品的概率,然后利用独立重复试验的概率公式可计算出结果;
(ii)由题意得出随机变量![]() 的可能取值,根据超几何分布的知识得出其分布列,由此可计算出随机变量
的可能取值,根据超几何分布的知识得出其分布列,由此可计算出随机变量![]() 的数学期望值.
的数学期望值.
(1)由题意知道:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以由图表知道:![]() ,
,
![]()
![]() ,
,
所以该设备![]() 的性能为丙级别;
的性能为丙级别;
(2)由图表知道:直径小于或等于![]() 的零件有
的零件有![]() 件,大于
件,大于![]() 的零件有
的零件有![]() 件,共计
件,共计![]() 件.
件.
(ⅰ)从设备![]() 的生产流水线上任取一件,取到次品的概率为
的生产流水线上任取一件,取到次品的概率为![]() ,
,
所以恰有一件次品的概率为![]() ;
;
(ⅱ)从![]() 件样品中任意抽取
件样品中任意抽取![]() 件,次品数
件,次品数![]() 可能取值为
可能取值为![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() ,
,![]() .
.
所以,随机变量![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
故![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
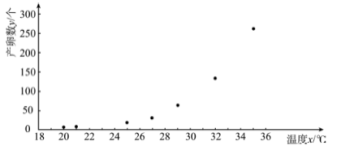
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在P地正西方向8km的A处和正东方向1km的B处各有一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F,为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设![]()
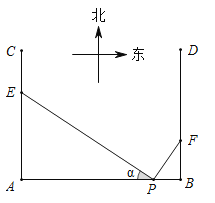
![]() Ⅰ
Ⅰ![]() 为减少对周边区域的影响,试确定E,F的位置,使
为减少对周边区域的影响,试确定E,F的位置,使![]() 与
与![]() 的面积之和最小;
的面积之和最小;
![]() Ⅱ
Ⅱ![]() 为节省建设成本,求使
为节省建设成本,求使![]() 的值最小时AE和BF的值.
的值最小时AE和BF的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为椭圆
为椭圆![]() 的左顶点,过
的左顶点,过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,
两点,![]() 是
是![]() 的中点.
的中点.
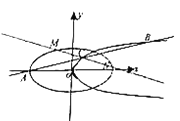
(1)求证:点![]() 的横坐标是定值,并求出该定值;
的横坐标是定值,并求出该定值;
(2)若直线![]() 过
过![]() 点,且倾斜角和直线
点,且倾斜角和直线![]() 的倾斜角互补,交椭圆于
的倾斜角互补,交椭圆于![]() 、
、![]() 两点,求
两点,求![]() 的值,使得
的值,使得![]() 的面积最大.
的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)如图,在五面体ABCDEF中,四边形EDCF是正方形,![]() .
.

(1)证明:![]() ;
;
(2)已知四边形ABCD是等腰梯形,且![]() ,求五面体ABCDEF的体积.
,求五面体ABCDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求直线
,求直线![]() 以及曲线
以及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)若![]() ,证明:函数
,证明:函数![]() 在区间
在区间![]() 上是单调增函数;
上是单调增函数;
(2)求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若函数![]() 的图像过原点,且
的图像过原点,且![]() 的导数
的导数![]() ,当
,当![]() 时,函数
时,函数![]() 过点
过点![]() 的切线至少有2条,求实数
的切线至少有2条,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com