
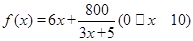 ;(2)当隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元.
;(2)当隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元.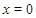 即可得
即可得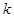 的值,可得建筑物每年的能消耗费用C与隔热层厚度x满足关系式,把隔热层建造费用
的值,可得建筑物每年的能消耗费用C与隔热层厚度x满足关系式,把隔热层建造费用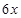 与20年的能耗费用相加再化简既得f(x)的表达式(注意不要忘记
与20年的能耗费用相加再化简既得f(x)的表达式(注意不要忘记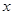 的取值范围);(2)把(1)中f(x)的表达式化成重要不等式的形式,利用重要不等式求f(x)的最小值和取得最小值时
的取值范围);(2)把(1)中f(x)的表达式化成重要不等式的形式,利用重要不等式求f(x)的最小值和取得最小值时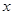 的取值.
的取值.

科目:高中数学 来源:不详 题型:解答题
 毫克)与时间
毫克)与时间 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后, 与
与 的函数关系式为
的函数关系式为 (
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题:
 (毫克)与时间
(毫克)与时间 (小时)之间的函数关系式;
(小时)之间的函数关系式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
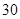 天内每件的销售价格
天内每件的销售价格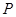 (元)与时间
(元)与时间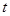 (天)的函数关系是
(天)的函数关系是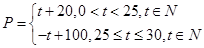 该商品的日销售量
该商品的日销售量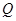 (件)与时间
(件)与时间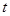 (天)的函数关系是
(天)的函数关系是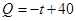
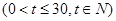 ,设商品的日销售额为
,设商品的日销售额为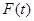 (销售量与价格之积)
(销售量与价格之积)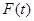 的解析式;
的解析式;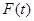 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在 段可近似地用解析式
段可近似地用解析式 来描述,从
来描述,从 点走到今天的
点走到今天的 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且 点和
点和 点正好关于直线
点正好关于直线 :
: 对称。老张预计这只股票未来的走势如图中虚线所示,这里
对称。老张预计这只股票未来的走势如图中虚线所示,这里 段与
段与 段关于直线
段关于直线 对称,
对称, 段是股价延续
段是股价延续 段的趋势(规律)走到这波上升行
段的趋势(规律)走到这波上升行
 。现在老张决定取点
。现在老张决定取点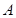
 ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,
,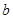 ,
, ,
, ,并且求得
,并且求得 。
。 ,
,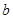 ,
, ,并回答股价什么时候见顶(即求
,并回答股价什么时候见顶(即求 点的横坐标)
点的横坐标) 点处的价格买入该股票3000股,到见顶处
点处的价格买入该股票3000股,到见顶处 点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
点的价格全部卖出,不计其它费用,这次操作他能赚多少元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com