
【题目】已知函数![]() ,关于
,关于![]() 的不等式
的不等式![]() 只有两个整数解,则实数
只有两个整数解,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】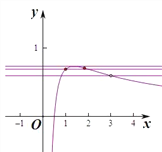
函数f(x)的定义域为(0,+∞),
则f′(x)= ![]() ,
,
当f′(x)>0得1ln(2x)>0,即ln(2x)<1,
即0<2x<e,即0<x<![]() ,
,
由f′(x)<0得1ln(2x)<0,得ln(2x)>1,
即2x>e,即x>![]() ,
,
即当x=![]() 时,函数f(x)取得极大值,同时也是最大值f(
时,函数f(x)取得极大值,同时也是最大值f(![]() )=
)=![]() =
=![]() ,
,
即当0<x<![]() 时,f(x)<
时,f(x)< ![]() 有一个整数解1,
有一个整数解1,
当x>![]() 时,0<f(x)<
时,0<f(x)< ![]() 有无数个整数解,
有无数个整数解,
若a=0,则![]() +af(x)>0得
+af(x)>0得![]() >0,此时有无数个整数解,不满足条件。
>0,此时有无数个整数解,不满足条件。
若a>0,
则由![]() +af(x)>0得f(x)>0或f(x)<a,
+af(x)>0得f(x)>0或f(x)<a,
当f(x)>0时,不等式由无数个整数解,不满足条件。
当a<0时,由![]() +af(x)>0得f(x)>a或f(x)<0,
+af(x)>0得f(x)>a或f(x)<0,
当f(x)<0时,没有整数解,
则要使当f(x)>a有两个整数解,
∵f(1)=ln2,f(2)= ![]() =ln2,f(3)=
=ln2,f(3)= ![]() ,
,
∴当f(x)ln2时,函数有两个整数点1,2,当f(x) ![]() 时,函数有3个整数点1,2,3
时,函数有3个整数点1,2,3
∴要使f(x)>a有两个整数解,
则![]() a<ln2,
a<ln2,
即ln2<a![]() ,
,
故选C.


科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c.已知 ![]() =
= ![]() .
.
(1)求角A的大小;
(2)当a=6时,求△ABC面积的最大值,并指出面积最大时△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探,由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用,勘探初期数据资料见如表:
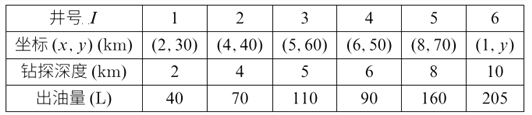
(参考公式和计算结果:
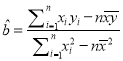 ,
, ![]() ,
, ![]() ,
, ![]() )
)
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() 的值,并估计
的值,并估计![]() 的预报值.
的预报值.
(2)现准备勘探新井![]() ,若通过1,3,5,7号并计算出的
,若通过1,3,5,7号并计算出的![]() ,
, ![]() 的值(
的值(![]() ,
, ![]() 精确到0.01)相比于(1)中的
精确到0.01)相比于(1)中的![]() ,
, ![]() ,值之差不超过10%,则使用位置最接近的已有旧井
,值之差不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(3)设出油量与勘探深度的比值![]() 不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数
不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】100名学生报名参加A、B两个课外活动小组,报名参加A组的人数是全体学生人数的 ![]() ,报名参加B组的人数比报名参加A组的人数多3,两组都没报名的人数是同时报名参加A、B两组人数的
,报名参加B组的人数比报名参加A组的人数多3,两组都没报名的人数是同时报名参加A、B两组人数的 ![]() 多1,求同时报名参加A、B两组人数( )
多1,求同时报名参加A、B两组人数( )
A.36
B.13
C.24
D.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在![]() 轴上,离心率等于
轴上,离心率等于![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点。
的焦点。
(1)求椭圆C的标准方程。
(2)已知点![]() 在椭圆C上,点A、B是椭圆C上不同于P、Q的两个动点,且满足:
在椭圆C上,点A、B是椭圆C上不同于P、Q的两个动点,且满足: ![]() 。试问:直线AB的斜率是否为定值?请说明理由。
。试问:直线AB的斜率是否为定值?请说明理由。
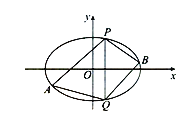
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( ) 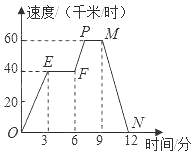
A.第3分时汽车的速度是40千米/时
B.第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车行驶了120千米
D.从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x2﹣mlnx,g(x)=x2﹣(m+1)x,m>0.
x2﹣mlnx,g(x)=x2﹣(m+1)x,m>0.
(1)求函数f(x)的单调区间;
(2)当m≥1时,讨论函数f(x)与g(x)图象的交点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=x2|x﹣a|(a∈R).21世纪教育网
(1)判定f(x)的奇偶性,并说明理由;
(2)当a≠0时,是否存在一点M(t,0),使f(x)的图象关于点M对称,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com