
【题目】下列函数中,既是偶函数,又在区间(0,+∞) 上单调递减的函数是( )
A.y=x﹣2
B.y=x﹣1
C.y=x2
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心, ![]() OA为半径作圆.
OA为半径作圆. 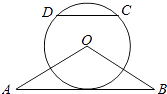
(1)证明:直线AB与⊙O相切;
(2)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12, 
(1)求线段PQ的长度;
(2)求证PQ⊥AD;
(3)求证:PQ∥平面CDD1C1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M是满足下列条件的函数f(x)的全体:存在非零常数T,对任意x∈R,有f(x+T)=Tf(x)成立.给出如下函数:①f(x)=x;②f(x)=2x;③f(x)= ![]() ;④f(x)=x2;则属于集合M的函数个数为( )
;④f(x)=x2;则属于集合M的函数个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的左焦点为F1有一小球A 从F1处以速度v开始沿直线运动,经椭圆壁反射(无论经过几次反射速度大小始终保持不变,小球半径忽略不计),若小球第一次回到F1时,它所用的最长时间是最短时间的5倍,则椭圆的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(n)=1+ ![]() ,g(n)=
,g(n)= ![]() ﹣
﹣ ![]() ,n∈N* .
,n∈N* .
(1)当n=1,2,3时,试比较f(n)与g(n)的大小关系;
(2)猜想f(n)与g(n)的大小关系,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com