
【题目】(本小题满分12分)
如图,已知四棱锥![]() 的底面为菱形,且
的底面为菱形,且![]() ,
, ![]()
![]() .
.
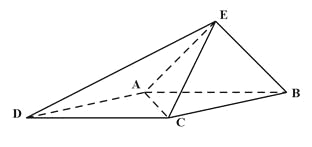
(I)求证:平面![]()
![]() 平面
平面![]() ;
;
(II)求二面角![]() 的余弦值.
的余弦值.
【答案】(I)证明:见解析
(II)二面角![]() 的余弦值为
的余弦值为![]()
【解析】本试题主要考查了面面垂直和二面角的求解的综合运用。
(1)根据已知条件找到线面垂直,然后利用面面垂直的判定定理得到其证明。
(2)合理的建立空间直角坐标系,然后表示出点的坐标和向量的坐标,借助于平面的法向量,得到向量的夹角,从而得到二面角的平面角的大小。
(I)证明:取![]() 的中点
的中点![]() ,连接
,连接![]()
![]()
![]() 为等腰直角三角形
为等腰直角三角形
![]() ……………………………………2分
……………………………………2分
又![]()
![]() 是等边三角形
是等边三角形
![]() ,又
,又![]()
![]() ,
, ![]() …………………………4分
…………………………4分
![]() ,又
,又![]()
![]() 平面
平面![]()
![]() 平面
平面![]() ;……………………………………6分
;……………………………………6分
(II)以![]() 中点
中点 ![]() 为坐标原点,以
为坐标原点,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系如图所示,
轴,建立空间直角坐标系如图所示,
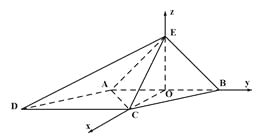
则![]()
![]() ……………………8分
……………………8分
设平面![]() 的法向量
的法向量![]()
![]()
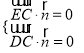 ,即
,即 ,解得
,解得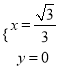 ,
,
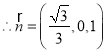
设平面![]() 的法向量
的法向量![]()
 ,即
,即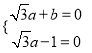 ,解得
,解得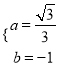 ,
,
 …………………………………………………………10分
…………………………………………………………10分
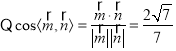
所以二面角![]() 的余弦值为
的余弦值为![]() …………………………12分
…………………………12分


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+alnx. (Ⅰ)当a=﹣2时,求函数f(x)的单调区间和极值;
(Ⅱ)若g(x)=f(x)+ ![]() 在[1,+∞)上是单调增函数,求实数a的取值范围.
在[1,+∞)上是单调增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c.已知 ![]() =
= ![]() .
.
(1)求角A的大小;
(2)当a=6时,求△ABC面积的最大值,并指出面积最大时△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中秋节即将到来,为了做好中秋节商场促销活动,某商场打算将进行促销活动的礼品盒重新设计.方案如下:将一块边长为10的正方形纸片![]() 剪去四个全等的等腰三角形
剪去四个全等的等腰三角形![]() ,
, ![]() ,
, ![]() ,
, ![]() 再将剩下的阴影部分折成一个四棱锥形状的包装盒
再将剩下的阴影部分折成一个四棱锥形状的包装盒![]() ,其中
,其中![]() 重合于点
重合于点![]() ,
, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合(如图所示).
重合(如图所示).
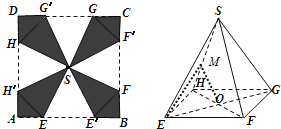
(1)求证:平面![]() 平面
平面![]() ;
;
(2)已知![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)判断并证明函数f(x)的奇偶性
(2)判断并证明当x∈(﹣1,1)时函数f(x)的单调性;
(3)在(2)成立的条件下,解不等式f(2x﹣1)+f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探,由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用,勘探初期数据资料见如表:
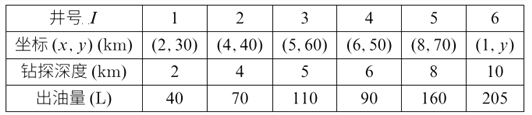
(参考公式和计算结果:
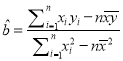 ,
, ![]() ,
, ![]() ,
, ![]() )
)
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() 的值,并估计
的值,并估计![]() 的预报值.
的预报值.
(2)现准备勘探新井![]() ,若通过1,3,5,7号并计算出的
,若通过1,3,5,7号并计算出的![]() ,
, ![]() 的值(
的值(![]() ,
, ![]() 精确到0.01)相比于(1)中的
精确到0.01)相比于(1)中的![]() ,
, ![]() ,值之差不超过10%,则使用位置最接近的已有旧井
,值之差不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(3)设出油量与勘探深度的比值![]() 不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数
不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】100名学生报名参加A、B两个课外活动小组,报名参加A组的人数是全体学生人数的 ![]() ,报名参加B组的人数比报名参加A组的人数多3,两组都没报名的人数是同时报名参加A、B两组人数的
,报名参加B组的人数比报名参加A组的人数多3,两组都没报名的人数是同时报名参加A、B两组人数的 ![]() 多1,求同时报名参加A、B两组人数( )
多1,求同时报名参加A、B两组人数( )
A.36
B.13
C.24
D.27
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com