
【题目】中秋节即将到来,为了做好中秋节商场促销活动,某商场打算将进行促销活动的礼品盒重新设计.方案如下:将一块边长为10的正方形纸片![]() 剪去四个全等的等腰三角形
剪去四个全等的等腰三角形![]() ,
, ![]() ,
, ![]() ,
, ![]() 再将剩下的阴影部分折成一个四棱锥形状的包装盒
再将剩下的阴影部分折成一个四棱锥形状的包装盒![]() ,其中
,其中![]() 重合于点
重合于点![]() ,
, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合(如图所示).
重合(如图所示).
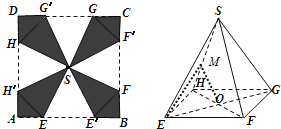
(1)求证:平面![]() 平面
平面![]() ;
;
(2)已知![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kx,g(x)= ![]() .
.
(1)求函数g(x)= ![]() 的单调区间;
的单调区间;
(2)若不等式f(x)≥g(x)在区间(0,+∞)上恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数,
是奇函数,
(1)求实数a的值;
(2)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求实数k的取值范围;
(3)设关于x的方程f(4x﹣b)+f(﹣2x+1)=0有实数根,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,抛物线
,抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上各取两个点,其坐标分别是
,从每条曲线上各取两个点,其坐标分别是![]() ,
, ![]() ,
, ![]() ,
, 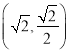 .
.
(1)求![]() ,
, ![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交于不同的两点
交于不同的两点![]() 且满足
且满足![]() ?若存在,求出直线方程;若不存在,请说明理由.
?若存在,求出直线方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com