练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的左焦点为F1有一小球A 从F1处以速度v开始沿直线运动，经椭圆壁反射（无论经过几次反射速度大小始终保持不变，小球半径忽略不计），若小球第一次回到F1时，它所用的最长时间是最短时间的5倍，则椭圆的离心率为（ ）

    A. B. C. D.

    【答案】C

    【解析】假设椭圆的长轴在x轴，短轴在y轴上，分为以下三种情况：

    球从F1沿x轴向左运动，碰到左顶点必然原路反弹，这时第一次回到F1的路程是2(a-c)；

    球从F1沿x轴向右运动，碰到右顶点必然原路反弹，这时第一次回到F1的路程是2(a+c)；

    球从F1沿x轴向上(或向下)运动，碰到椭圆上的点A，反弹后经过椭圆的另一个焦点F2，再弹到椭圆上的点B，经过点B反弹后经过焦点F2，此时小球经过的路程是4a.

    综上所述，从点F1沿直线出发，经椭圆反弹后第一次回到点F1时，小球经过的最大路程是4a，最小路程是2(a-c)，

    所以由题意可知4a=10(a-c)，即6a=10c，得，

    所以椭圆的离心率为.

    本题选择C选项.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】100名学生报名参加A、B两个课外活动小组，报名参加A组的人数是全体学生人数的 ，报名参加B组的人数比报名参加A组的人数多3，两组都没报名的人数是同时报名参加A、B两组人数的 多1，求同时报名参加A、B两组人数（ ）
    A.36
    B.13
    C.24
    D.27

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数中，既是偶函数，又在区间（0，+∞） 上单调递减的函数是（ ）
    A.y=x﹣2
    B.y=x﹣1
    C.y=x2
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知极坐标系的极点与直角坐标系的原点重合，极轴与轴的正半轴重合，圆的极坐标方程为，直线的参数方程为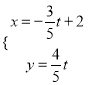（为参数）．

    （Ⅰ）若， 是直线与轴的交点， 是圆上一动点，求的最大值；

    （Ⅱ）若直线被圆截得的弦长等于圆的半径倍，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C1的参数方程是 (φ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ＝2.正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为.

    (1)求点A，B，C，D的直角坐标；

    (2)设P为C1上任意一点，求|PA|2＋|PB|2＋|PC|2＋|PD|2的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （Ⅰ）若，求的单调区间；（Ⅱ）若有最大值3，求的值；（Ⅲ）若的值域是，求的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的函数f（x）=x2|x﹣a|（a∈R）．21世纪教育网
    （1）判定f（x）的奇偶性，并说明理由；
    （2）当a≠0时，是否存在一点M（t，0），使f（x）的图象关于点M对称，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知：f（x）=lg（ax﹣bx）（a＞1＞b＞0）．
    （1）求f（x）的定义域；
    （2）判断f（x）在其定义域内的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，分别是的中点，平面平面，，是边长为2的正三角形，.

    （1）求证：平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案