
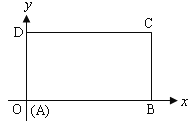
【题目】在平面直角坐标系中,已知矩形![]() 的长为2,宽为1,
的长为2,宽为1,![]() .
.![]() 边分别在
边分别在![]() 轴.
轴.![]() 轴的正半轴上,
轴的正半轴上,![]() 点与坐标原点重合(如图所示)。将矩形折叠,使
点与坐标原点重合(如图所示)。将矩形折叠,使![]() 点落在线段
点落在线段![]() 上。
上。

(1)若折痕所在直线的斜率为![]() ,试求折痕所在直线的方程;
,试求折痕所在直线的方程;
(2)当![]() 时,求折痕长的最大值;
时,求折痕长的最大值;
(3)当![]() 时,折痕为线段
时,折痕为线段![]() ,设
,设![]() ,试求
,试求![]() 的最大值。
的最大值。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)对k=0,![]() 分类讨论,将矩形折叠后
分类讨论,将矩形折叠后![]() 点落在线段
点落在线段![]() 上的点记为
上的点记为![]() ,先求G的坐标,再求折痕所在的直线与
,先求G的坐标,再求折痕所在的直线与![]() 的交点坐标,写出直线的点斜式方程.(2) 先求出折痕直线交
的交点坐标,写出直线的点斜式方程.(2) 先求出折痕直线交![]() 于点
于点![]() ,交
,交![]() 轴于
轴于![]() ,再求
,再求![]() 的最大值,即得折痕长的最大值.(3)先求得
的最大值,即得折痕长的最大值.(3)先求得![]() ,再求t的表达式和其最大值.
,再求t的表达式和其最大值.
(1) ①当![]() 时,此时
时,此时![]() 点与
点与![]() 点重合, 折痕所在的直线方程
点重合, 折痕所在的直线方程![]()
②当![]() 时,将矩形折叠后
时,将矩形折叠后![]() 点落在线段
点落在线段![]() 上的点记为
上的点记为![]() ,
,
所以![]() 与
与![]() 关于折痕所在的直线对称,
关于折痕所在的直线对称,
有![]()
![]()
![]()
![]()
![]()
故![]() 点坐标为
点坐标为![]() ,
,
从而折痕所在的直线与![]() 的交点坐标(线段
的交点坐标(线段![]() 的中点)为
的中点)为![]()
折痕所在的直线方程![]() ,即
,即![]()
由①②得折痕所在的直线方程为:![]()
(2)当![]() 时,折痕的长为2;
时,折痕的长为2;
当![]() 时,折痕直线交
时,折痕直线交![]() 于点
于点![]() ,交
,交![]() 轴于
轴于![]()
∵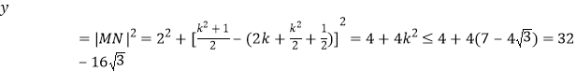
∴折痕长度的最大值为![]() 。
。
而![]() ,故折痕长度的最大值为
,故折痕长度的最大值为![]()
(3)当![]() 时,折痕直线交
时,折痕直线交![]() 于
于![]() ,交
,交![]() 轴于
轴于![]()
∵![]() ∴
∴![]()
∵![]() ∴
∴![]() (当且仅当
(当且仅当![]() 时取“=”号)
时取“=”号)
∴当![]() 时,
时,![]() 取最大值,
取最大值,![]() 的最大值是
的最大值是![]() 。
。


科目:高中数学 来源: 题型:
【题目】收入是衡量一个地区经济发展水平的重要标志之一,影响收入的因素有很多,为分析学历对收入的作用,某地区调查机构欲对本地区进行了此项调查.

(1)你认为应采用何种抽样方法进行调查?
(2)经调查得到本科学历月均收入条形图如图,试估算本科学历月均收入![]() 的值?
的值?
(3)设学年为![]() ,令
,令![]() ,月均收入为
,月均收入为![]() ,已知调查机构调查结果如下表
,已知调查机构调查结果如下表
学历 (年) | 小学 | 初中 | 高中 | 本科 | 硕士生 | 博士生 |
| 6 | 9 | 12 | 16 | 19 | 22 |
| 2.0 | 2.7 | 3.7 | 5.8 | 7.8 | |
| 2210 | 2410 | 2910 |
| 6960 |
从散点图中可看出![]() 和
和![]() 的关系可以近似看成是一次函数图像. 若回归直线方程为
的关系可以近似看成是一次函数图像. 若回归直线方程为![]() ,试预测博士生的平均月收入.
,试预测博士生的平均月收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在
定义在![]() 上且满足下列两个条件:
上且满足下列两个条件:
①对任意![]() 都有
都有![]() ;
;
②当![]() 时,有
时,有![]() ,
,
(1)求![]() ,并证明函数
,并证明函数![]() 在
在![]() 上是奇函数;
上是奇函数;
(2)验证函数![]() 是否满足这些条件;
是否满足这些条件;
(3)若![]() ,试求函数
,试求函数![]() 的零点.
的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,前n项和为Sn , 且Sn= ![]() ,数列{bn}的前n项和为Tn , 且bn=
,数列{bn}的前n项和为Tn , 且bn= ![]()
(1)求数列{an}的通项公式;
(2)是否存在m,n∈N* , 使得Tn=am , 若存在,求出所有满足题意的m,n,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 在平行四边形ABCD中,A(1,1),![]() =(6,0),点M是线段AB的中点,线段CM与BD交于点P.(1) 若
=(6,0),点M是线段AB的中点,线段CM与BD交于点P.(1) 若![]() =(3,5),求点C的坐标;(2) 当|
=(3,5),求点C的坐标;(2) 当|![]() |=|
|=|![]() |时,求点P的轨迹.
|时,求点P的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足:对任意x,y∈R,都有f(x+y)=f(x)f(y)﹣f(x)﹣f(y)+2成立,且x>0时,f(x)>2,
(1)求f(0)的值,并证明:当x<0时,1<f(x)<2.
(2)判断f(x)的单调性并加以证明.
(3)若函数g(x)=|f(x)﹣k|在(﹣∞,0)上递减,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com