
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面
,底面![]() 为平行四边形,
为平行四边形,![]() ,
,![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由![]() 平面
平面![]() ,可得到
,可得到![]() ,结合
,结合![]() ,根据线面垂直的判定定理即可得到
,根据线面垂直的判定定理即可得到![]() 平面
平面![]() ,从而可得出
,从而可得出![]() ;(2)首先以
;(2)首先以![]() 三直线为
三直线为![]() 轴,建立空间直角坐标系,可设
轴,建立空间直角坐标系,可设![]() ,从而可确定图形上各点的坐标,利用向量垂直数量积为零列方程组求出平面
,从而可确定图形上各点的坐标,利用向量垂直数量积为零列方程组求出平面![]() 的法向量,设直线
的法向量,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则根据
,则根据![]() 及空间向量夹角余弦公式,即可求得
及空间向量夹角余弦公式,即可求得![]() .
.
试题解析:(1)![]() 平面
平面![]() 平面
平面![]() ,即
,即![]() ,又
,又![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
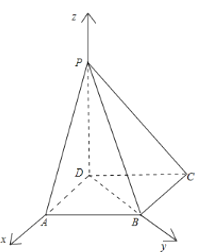
(2)分别以![]() 三直线为
三直线为![]() 轴,建立如图所示空间直角坐标系,设
轴,建立如图所示空间直角坐标系,设![]() ,则
,则![]() ,
,![]() ,
,![]()
![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则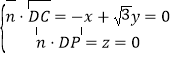 ,取
,取![]() ,记直线
,记直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,
,![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【方法点晴】本题主要考查线面垂直的判定与性质,以及利用空间向量求线面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】设满足以下两个条件的有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 阶“期待数列”:
阶“期待数列”:
①![]() ;
;
②![]() .
.
(![]() )分别写出一个单调递增的
)分别写出一个单调递增的![]() 阶和
阶和![]() 阶“期待数列”.
阶“期待数列”.
(![]() )若某
)若某![]() 阶“期待数列”是等差数列,求该数列的通项公式.
阶“期待数列”是等差数列,求该数列的通项公式.
(![]() )记
)记![]() 阶“期待数列”的前
阶“期待数列”的前![]() 项和为
项和为![]() ,试证:
,试证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)过点P(1,
=1(a>b>0)过点P(1, ![]() ).离心率为
).离心率为![]() .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A,B两点.
①若直线l过椭圆C的右焦点,记△ABP三条边所在直线的斜率的乘积为t.
求t的最大值;
②若直线l的斜率为![]() ,试探究OA2+ OB2是否为定值,若是定值,则求出此
,试探究OA2+ OB2是否为定值,若是定值,则求出此
定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经销一批进价为每件30元的商品,在市场试销中发现,此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系:
x | 30 | 40 | 45 | 50 |
y | 60 | 30 | 15 | 0 |
在所给的坐标图纸中,根据表中提供的数据,描出实数对(x,y)的对应点,并确定y与x的一个函数关系式;

(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少元时,才能获得最大日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
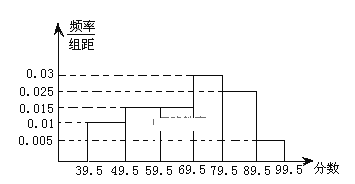
【题目】如图,从参加环保知识竞赛的学生中抽出![]() 名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:
(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(![]() 分及以上为及格)和平均数?
分及以上为及格)和平均数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知矩形![]() 的长为2,宽为1,
的长为2,宽为1,![]() .
.![]() 边分别在
边分别在![]() 轴.
轴.![]() 轴的正半轴上,
轴的正半轴上,![]() 点与坐标原点重合(如图所示)。将矩形折叠,使
点与坐标原点重合(如图所示)。将矩形折叠,使![]() 点落在线段
点落在线段![]() 上。
上。

(1)若折痕所在直线的斜率为![]() ,试求折痕所在直线的方程;
,试求折痕所在直线的方程;
(2)当![]() 时,求折痕长的最大值;
时,求折痕长的最大值;
(3)当![]() 时,折痕为线段
时,折痕为线段![]() ,设
,设![]() ,试求
,试求![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为角A,B,C所对的三边,a2﹣(b﹣c)2=bc,
(1)求角A;
(2)若BC=2 ![]() ,角B等于x,周长为y,求函数y=f(x)的取值范围.
,角B等于x,周长为y,求函数y=f(x)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com