
【题目】已知函数![]() 定义在
定义在![]() 上且满足下列两个条件:
上且满足下列两个条件:
①对任意![]() 都有
都有![]() ;
;
②当![]() 时,有
时,有![]() ,
,
(1)求![]() ,并证明函数
,并证明函数![]() 在
在![]() 上是奇函数;
上是奇函数;
(2)验证函数![]() 是否满足这些条件;
是否满足这些条件;
(3)若![]() ,试求函数
,试求函数![]() 的零点.
的零点.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)过点P(1,
=1(a>b>0)过点P(1, ![]() ).离心率为
).离心率为![]() .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A,B两点.
①若直线l过椭圆C的右焦点,记△ABP三条边所在直线的斜率的乘积为t.
求t的最大值;
②若直线l的斜率为![]() ,试探究OA2+ OB2是否为定值,若是定值,则求出此
,试探究OA2+ OB2是否为定值,若是定值,则求出此
定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经销一批进价为每件30元的商品,在市场试销中发现,此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系:
x | 30 | 40 | 45 | 50 |
y | 60 | 30 | 15 | 0 |
在所给的坐标图纸中,根据表中提供的数据,描出实数对(x,y)的对应点,并确定y与x的一个函数关系式;

(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少元时,才能获得最大日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
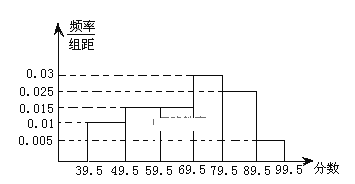
【题目】如图,从参加环保知识竞赛的学生中抽出![]() 名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:
(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(![]() 分及以上为及格)和平均数?
分及以上为及格)和平均数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(3, ![]() ),点B的极坐标为(6,
),点B的极坐标为(6, ![]() ),曲线C:(x﹣1)2+y2=1
),曲线C:(x﹣1)2+y2=1
(1)求曲线C和直线AB的极坐标方程;
(2)过点O的射线l交曲线C于M点,交直线AB于N点,若|OM||ON|=2,求射线l所在直线的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知矩形![]() 的长为2,宽为1,
的长为2,宽为1,![]() .
.![]() 边分别在
边分别在![]() 轴.
轴.![]() 轴的正半轴上,
轴的正半轴上,![]() 点与坐标原点重合(如图所示)。将矩形折叠,使
点与坐标原点重合(如图所示)。将矩形折叠,使![]() 点落在线段
点落在线段![]() 上。
上。

(1)若折痕所在直线的斜率为![]() ,试求折痕所在直线的方程;
,试求折痕所在直线的方程;
(2)当![]() 时,求折痕长的最大值;
时,求折痕长的最大值;
(3)当![]() 时,折痕为线段
时,折痕为线段![]() ,设
,设![]() ,试求
,试求![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
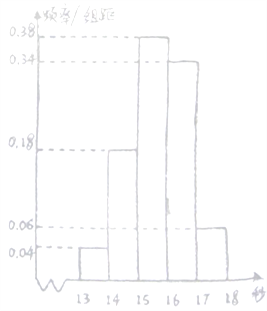
(1)请根据频率分布直方图估计该组数据的众数和中位数(精确到0.1);
(2)从成绩介于![]() 和
和![]() 两组的人中任取2人,求两人分布来自不同组的概率.
两组的人中任取2人,求两人分布来自不同组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com