
【题目】若偶函数y=f(x)(![]() 满足f(1+x)=f(1-x),且当
满足f(1+x)=f(1-x),且当![]() 时,
时,![]() ,则函数g(x)=f(x)-
,则函数g(x)=f(x)-![]() 的零点个数为_________个.
的零点个数为_________个.
【答案】10
【解析】
运用函数的对称性和奇偶性,确定函数y=f(x)的周期,构造函数y=f(x),h(x)=|lgx|,则函数g(x)=f(x)﹣|lgx|的零点问题转化为图象的交点问题,结合图象,即可得到结论.
∵偶函数y=f(x)满足f(1+x)=f(1﹣x),
即函数f(x)关于x=1对称,即有f(x+2)=f(﹣x)=f(x),
则函数y=f(x)的周期为2,
构造函数y=f(x),h(x)=|lgx|,
则函数g(x)=f(x)﹣|lgx|的零点问题转化为图象的交点问题,
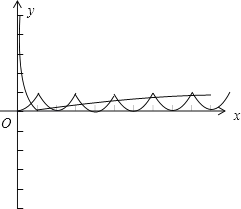
画出函数图象,如图,
由于f(x)的最大值1,
所以x>10时,图象没有交点,在(0,1)上有一个交点,(1,3),(3,5),(5,7),(7,9)上各有两个交点,在(9,10)上有一个交点,故共有10个交点,
即函数零点的个数为10.
故答案为10.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+1|(a∈R),g(x)=|2x﹣1|+2.
(1)若a=1,证明:不等式f(x)≤g(x)对任意的x∈R成立;
(2)若对任意的m∈R,都有t∈R,使得f(m)=g(t)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校准备将![]() 名同学全部分配到运动会的田径、拔河和球类
名同学全部分配到运动会的田径、拔河和球类![]() 个不同项目比赛做志愿者,每个项目至少
个不同项目比赛做志愿者,每个项目至少![]() 名,则不同的分配方案有________种(用数字作答).
名,则不同的分配方案有________种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为双曲线
为双曲线![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴的上方交双曲线C于点M,且
轴的上方交双曲线C于点M,且![]()
(1)求双曲线C的方程;
(2)过双曲线C上任意一点P作该双曲线两条渐近线的垂线,垂足分别为![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 准线为
准线为![]() ,焦点为
,焦点为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上位于第一象限的动点,直线
上位于第一象限的动点,直线![]() (
(![]() 为坐标原点)交
为坐标原点)交![]() 于
于![]() 点,直线
点,直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为线段
为线段![]() 中点.
中点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)试问直线![]() 的斜率是否为定值,若是,求出该值;若不是,说明理由.
的斜率是否为定值,若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
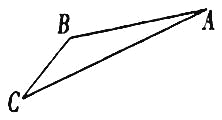
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com