
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是 ( ).
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-10练习卷(解析版) 题型:选择题
如图所示,程序框图运行后输出k的值是( ).
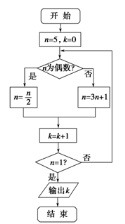
A.4 B.5 C.6 D.7
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评6练习卷(解析版) 题型:解答题
如图所示,已知椭圆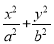 =1(a>b>0)的右焦点为F2(1,0),点A
=1(a>b>0)的右焦点为F2(1,0),点A 在椭圆上.
在椭圆上.
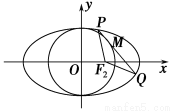
(1)求椭圆方程;
(2)点M(x0,y0)在圆x2+y2=b2上,点M在第一象限,过点M作圆x2+y2=b2的切线交椭圆于P、Q两点,问|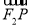 |+|
|+| |+|
|+| |是否为定值?如果是,求出该定值;如果不是,说明理由.
|是否为定值?如果是,求出该定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评5练习卷(解析版) 题型:解答题
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
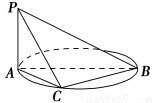
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评5练习卷(解析版) 题型:选择题
如图所示,在正三棱柱ABC-A1B1C1中,AB=1.若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( ).

A. 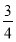 B.
B.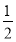 C.
C.  D.1
D.1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(解析版) 题型:解答题
已知单调递增的等比数列{an}满足:
a2+a3+a4=28,且a3+2是a2和a4的等差中项.
(1)求数列{an}的通项公式an;
(2)令bn=anlog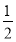 an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.
an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评3练习卷(解析版) 题型:填空题
设△ABC的内角A,B,C的对边分别为a,b,c,且a=1,b=2,cos C=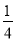 ,则sin B=________.
,则sin B=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评1练习卷(解析版) 题型:选择题
设a,b是两个非零向量,下列选项正确的是( ).
A.若|a+b|=|a|-|b|,则a⊥b
B.若a⊥b,则|a+b|=|a|-|b|
C.若|a+b|=|a|-|b|,则存在实数λ,使得b=λa
D.若存在实数λ,使得b=λa,则|a+b|=|a|-|b|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com