
如图1-2-13,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较其异同点.
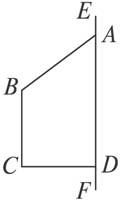
图1-2-13
(1)当点A在图1-2-14射线DE的位置时,绕EF旋转一周所得几何体为底面半径为CD的圆柱和圆锥拼成,其三视图如图1-2-15:
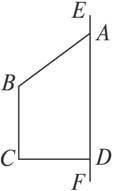
图1-2-14
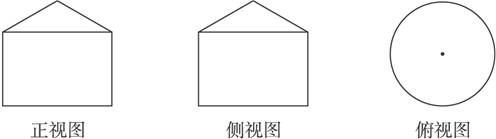
图1-2-15
(2)当点A在图1-2-16射线DE的位置,即B到EF所作垂线的垂足时,旋转后几何体为圆柱,其三视图如图1-2-17:
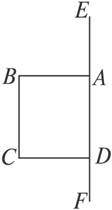
图1-2-16

图1-2-17
(3)当点A位于如图1-2-18所示位置时,其旋转所得几何体为圆柱中挖去同底的圆锥,其三视图如图1-2-19.
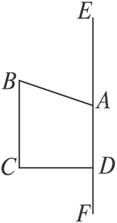
图1-2-18
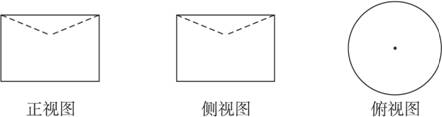
图1-2-19
(4)当点A位于点D时,如图1-2-20,此时旋转体为圆柱中挖去一个同底等高的圆锥,其三视图如图1-2-21.
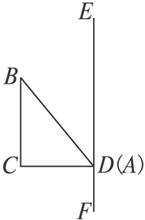
图1-2-20

图1-2-21
本题关键在于要对A选在射线DE上的不同位置分别讨论,看旋转后的几何体可由哪些简单几何体构成. 本题充分考查了空间想象力.由轴截面想到旋转体,由旋转所得组合体画出三视图,综合性很强,同时也显示了旋转体的三视图特点,即正视图与侧视图完全相同,并且俯视图为圆.故旋转体的三视图可简化为“二视图”.


科目:高中数学 来源: 题型:
(本题13分)将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结部分线段后围成一个空间几何体,如图2所示.
 (1)求证:
(1)求证:![]() ;
;
(2)求二面角D—BF—E的大小;
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市高三毕业班质量检查理科数学试卷(解析版) 题型:解答题
(本小题满分13分)
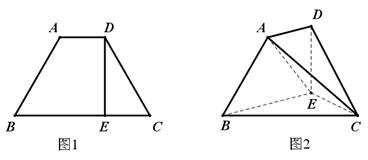
如图1,在等腰梯形 中,
中,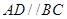 ,
,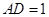 ,
,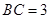 ,
,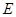 为
为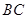 上一点,
上一点, 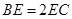 ,且
,且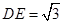 .将梯形
.将梯形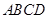 沿
沿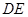 折成直二面角
折成直二面角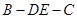 ,如图2所示.
,如图2所示.
(Ⅰ)求证:平面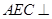 平面
平面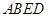 ;
;
(Ⅱ)设点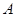 关于点
关于点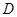 的对称点为
的对称点为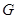 ,点
,点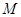 在
在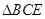 所在平面内,且直线
所在平面内,且直线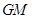 与平面
与平面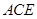 所成的角为
所成的角为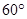 ,试求出点
,试求出点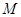 到点
到点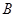 的最短距离.
的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
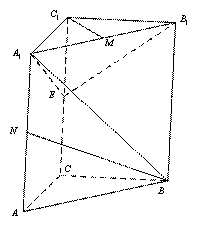 (本小题满分13分) 如图所示,直三棱柱ABC-A1B1C1中,CA=CB=2,
(本小题满分13分) 如图所示,直三棱柱ABC-A1B1C1中,CA=CB=2, ![]() 棱
棱![]() ,E、M、N分别是CC1、A1B1、AA1的中点.
,E、M、N分别是CC1、A1B1、AA1的中点.
(1)求证:![]() ;
;
(2) 求BN的长;
(3) 求二面角![]() 平面角的余弦值.
平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
 如图所示,直三棱柱ABC-A1B1C1中,CA=CB,
如图所示,直三棱柱ABC-A1B1C1中,CA=CB, ![]() E、M分别是CC1、A1B1的中点.
E、M分别是CC1、A1B1的中点.
(1)求证:![]() ;
;
(2)求证:C1M //平面AB1E.
查看答案和解析>>
科目:高中数学 来源: 题型:
. (本小题共13分)
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和
BC边上的点,且满足![]() ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
(Ⅰ) 试判断翻折后直线AB与平面DEF的位置关系,并说明理由 ;
(Ⅱ) 求二面角B-AC-D的平面角的正切值.
 | |||
 | |||
图(1) 图(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com