
| A. | 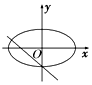 | B. | 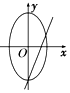 | C. | 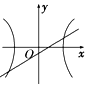 | D. |  |
分析 通过讨论A,B的值,得到$\frac{{x}^{2}}{B}-\frac{{y}^{2}}{A}=1$表示的圆锥曲线形状;将直线方程Bx-y+A=0变形为斜截式判断出其斜率及纵截距,由两种曲线的特点,选出图象.
解答 解:当A>0,B>0时,$\frac{{x}^{2}}{B}-\frac{{y}^{2}}{A}=1$表示焦点在x轴的双曲线,
方程Bx-y+A=0即为y=Bx+A其斜率为B,纵截距为A,
∴选项C,D错;
当A<0,B>0,且|A|>|B|时,$\frac{{x}^{2}}{B}-\frac{{y}^{2}}{A}=1$表示焦点在y轴的椭圆,
方程Bx-y+A=0即为y=Bx+A其斜率为B,纵截距为A,
故选项A错;
当A<0,B>0,且|A|<|B|时,$\frac{{x}^{2}}{B}-\frac{{y}^{2}}{A}=1$表示焦点在x轴的椭圆,
方程Bx-y+A=0即为y=Bx+A其斜率为B,纵截距为A.
故选B.
点评 解决已知曲线的方程选择其图象的题目,一般先根据方程研究方程表示的曲线的性质,再根据曲线的性质选择出合适的图象.


科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在平面直角坐标系下,直线 (
(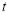 为参数),以原点
为参数),以原点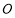 为极点,以
为极点,以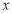 轴为非负半轴为极轴,取相同长度单位建立极坐标系,曲线
轴为非负半轴为极轴,取相同长度单位建立极坐标系,曲线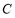 的极坐标方程为
的极坐标方程为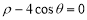 .
.
(Ⅰ)写出直线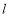 的普通方程和曲线
的普通方程和曲线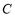 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线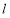 与曲线
与曲线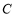 交于
交于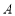 ,
,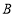 两点,求
两点,求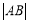 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x2-2|x|-1.
已知函数f(x)=x2-2|x|-1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
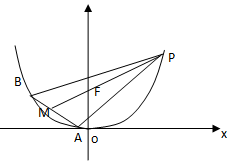 已知△ABP的三个顶点都在抛物线C:x2=4y上,P在第一象限,如图.F为抛物线C的焦点,点M为AB的中点,$\overrightarrow{PF}$=3$\overrightarrow{FM}$,|PF|=3,求直线AB的方程.
已知△ABP的三个顶点都在抛物线C:x2=4y上,P在第一象限,如图.F为抛物线C的焦点,点M为AB的中点,$\overrightarrow{PF}$=3$\overrightarrow{FM}$,|PF|=3,求直线AB的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com