已知二次函数f(x)=ax2+bx(a,b为常数且a≠0)满足f(1-x)=f(1+x),且方程f(x)=x有等根.
(1)求f(x)的解析式;
(2)设g(x)=1-2f(x)(x>1)的反函数为g-1(x),若g-1(22x)>m(3-2x)对x∈[1,2]恒成立,求实数m的取值范围.
解:(1)∵f(1-x)=f(1+x),
∴函数的对称轴为x=1,即

=1
∵方程f(x)=x有等根,∴△=(b-1)
2=0
∴b=1,a=-

∴
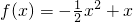
.
(2)由(1)得g(x)=x
2-2x+1,
当x>1时,y=(x-1)
2>0?x=1+
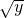
?g
-1(x)=1+

(x>0),
∵g
-1(2
2x)>m(3-2
x)对x∈[1,2]恒成立,
即1+2
x>m(3-2
x)对x∈[1,2]恒成立,
令t=2
x,则(m+1)t+1-3m>0,对t∈[2,4]恒成立,
∴
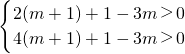
?-5<m<3.
分析:(1)先由f(1-x)=f(1+x)得函数对称轴,再由方程f(x)=x有等根,得方程f(x)=x的判别式等于零,最后解方程即可;
(2)由(1)得出g(x)的解析式,再将x用y表示,最后交换x、y,即可求出反函数的解析式,从而得1+2
x>m(3-2
x)对x∈[1,2]恒成立,t=2
x,转化成关于t的一次函数恒成立问题,根据函数在[2,4]上的单调性建立不等式,从而求出所求.
点评:本题考查了二次函数解析式的求法,解题时要熟练掌握二次函数的图象特征,还考查了反函数,以及反函数与原函数的之间的关系,同时考查了恒成立问题和最值问题,是一道综合题.

 =1
=1
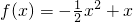 .
.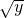 ?g-1(x)=1+
?g-1(x)=1+ (x>0),
(x>0),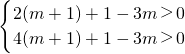


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案