
分析 (Ⅰ)由已知数列递推式可得an+1an+2=4Sn+1-1,与原递推式作差可得an+2-an=4,说明{a2n-1}是首项为1,公差为4的等差数列,{a2n}是首项为3,公差为4的等差数列,分别求出通项公式后可得{an}的通项公式;
(Ⅱ)由等差数列的前n项和求得Sn,取其倒数后利用放缩法证明$\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{S_n}$<2.
解答 (I)解:由题设,anan+1=4Sn-1,得an+1an+2=4Sn+1-1.
两式相减得an+1(an+2-a)=4an+1.
由于an+1≠0,∴an+2-an=4.
由题设,a1=1,a1a2=4S1-1,可得a2=3.
故可得{a2n-1}是首项为1,公差为4的等差数列,a2n-1=4n-3=2(2n-1)-1;
{a2n}是首项为3,公差为4的等差数列,a2n=4n-1=2•2n-1.
∴${a_n}=2n-1({n∈{N^*}})$;
(Ⅱ)证明:${S_n}=\frac{{n({1+2n-1})}}{2}={n^2}$,
当n>1时,由$\frac{1}{n^2}<\frac{1}{{n({n-1})}}=\frac{1}{n-1}-\frac{1}{n}$,得
$\frac{1}{S_1}+\frac{1}{S_2}+…+\frac{1}{S_n}=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+…+\frac{1}{n^2}$$<\frac{1}{1}+\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n-1}-\frac{1}{n}=2-\frac{1}{n}$,
∴$\frac{1}{S_1}+\frac{1}{S_2}+…+\frac{1}{S_n}<2$.
点评 本题考查数列递推式,考查了等差关系的确定,考查等差数列前n项和的求法,训练了利用放缩法证明数列不等式,是中档题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 是减函数 | B. | 是增函数或减函数 | ||
| C. | 是增函数 | D. | 未必是增函数或减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx+ex | B. | cosx+ex | C. | -sinx+ex | D. | -cosx+ex |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
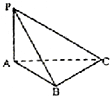 如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB=1,BC=$\sqrt{2}$,若三棱锥P-ABC的四个顶点在同一个球面上,则这个球的表面积为( )
如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB=1,BC=$\sqrt{2}$,若三棱锥P-ABC的四个顶点在同一个球面上,则这个球的表面积为( )| A. | π | B. | 2π | C. | 3π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40种 | B. | 48种 | C. | 52种 | D. | 60种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com