
数列{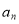 }是等差数列且
}是等差数列且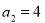 ,
,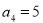 ,数列{
,数列{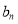 }的前
}的前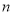 项和为
项和为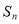 ,且
,且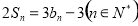 .
.
(Ⅰ)求数列{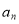 },{
},{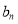 }的通项公式;
}的通项公式;
(Ⅱ)求数列{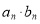 }的前n项和为
}的前n项和为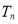 .
.
(1) ,
,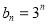 ;(2)
;(2)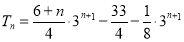
【解析】
试题分析:(1)根据等差数列的首项和公差求通项公式;根据等比数列的首项和公比求通项公式;注意题中限制条件;(2)给出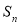 与
与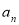 的关系,求
的关系,求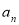 ,常用思路:一是利用
,常用思路:一是利用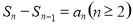 转化为
转化为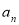 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为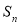 的递推关系,先求出
的递推关系,先求出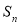 与
与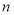 的关系,再求
的关系,再求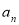 ;由
;由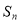 推
推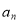 时,别漏掉
时,别漏掉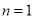 这种情况,大部分学生好遗忘;(3)一般地,如果数列
这种情况,大部分学生好遗忘;(3)一般地,如果数列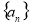 是等差数列,
是等差数列,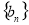 是等比数列,求数列
是等比数列,求数列
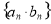 的前
的前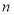 项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列
项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列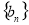 的公比,然后做差求解.
的公比,然后做差求解.
试题解析:解(1)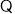 数列
数列 是等差数列且
是等差数列且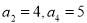 ,
,
 ,截得
,截得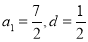 ,
,
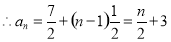
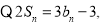 ①
①
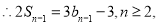 ②
②
①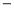 ②,得
②,得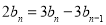

又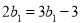 ,解得
,解得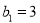 ,
,

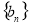 是以3为首项,3为公比的等比数列,
是以3为首项,3为公比的等比数列,
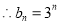
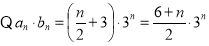 ,
,
 ,①
,①
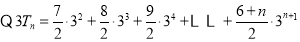 ,②
,②
①﹣②,﹣2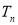 =
=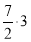 +
+ (32+33+…+3n)﹣
(32+33+…+3n)﹣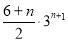
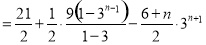
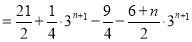
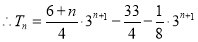
考点:(1)求等差数列、等比数列的通项公式;(2)错位相减求和.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016届河北省高一下学期期中考试数学卷(解析版) 题型:选择题
已知数列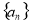 为等差数列,若
为等差数列,若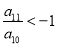 ,且它们的前n项和
,且它们的前n项和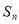 有最大值,
有最大值,
则使得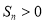 的n的最大值为( ).
的n的最大值为( ).
(A)11 (B)19 (C)20 (D)21
查看答案和解析>>
科目:高中数学 来源:2016届江西省高一下学期第二次月考数学试卷(解析版) 题型:解答题
递减的等差数列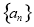 的前n项和为
的前n项和为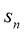 ,若
,若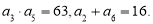
(1)求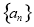 的等差通项;
的等差通项;
(2)当n为多少时,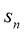 取最大值,并求出其最大值;
取最大值,并求出其最大值;
(3)求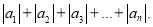
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com