
设 表示两条直线,
表示两条直线, 表示两个平面,则下列命题是真命题的是( )
表示两个平面,则下列命题是真命题的是( )
A.若 , , ∥ ∥ ,则 ,则 ∥ ∥ |
B.若 |
C.若 ∥ ∥ , , ,则 ,则 |
D.若 |
D
解析试题分析:对于选项A,如果一条直线平行与这个平面,那么它和平面内的任何一条直线可能平行,也可能异面,故错误。
对于B,直线C有可能就在平面 内,故错误。
内,故错误。
对于C,由于两个平面垂直,一条直线平行与其中的一个平面,则这条直线与另一个平面可能平行,或者垂直,因此错误。
对于D,根据面面平行的判定定理可知, 经过了
经过了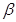 的一条垂线,因此面面垂直, 故选D.
的一条垂线,因此面面垂直, 故选D.
考点:本试题考查了空间中点线面的位置关系知识点。
点评:解决该试题的关键是能够熟练的运用线面的,平行和垂直,和面面垂直的判定定理和性质定理来证明线面平行和面面垂直问题。也可以借助于生活中的实物图来分析得到,常用的为正方体或者长方体,属于基础题。


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:单选题
设 是三个不重合的平面,l是直线,给出下列命题:
是三个不重合的平面,l是直线,给出下列命题:
①若 ,则
,则 ; ②若
; ②若
③若l上存在两点到 的距离相等,则
的距离相等,则 ; ④若
; ④若
其中正确的命题是( )
| A.①② | B.②③ | C.②④ | D.③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知直线l垂直平面a,垂足为O.在矩形ABCD中AD=1,AB=2,若点A在l上移动,点 B在平面a上移动,则O、D两点间的最大距离为
A.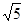 | B.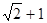 | C.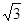 | D.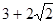 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
椭圆 的长轴为
的长轴为
 ,短轴为
,短轴为
 ,将椭圆沿y轴折成一个二面角,使得
,将椭圆沿y轴折成一个二面角,使得 点在平面
点在平面

 上的射影恰好为椭圆的右焦点,则该二面角的大小为( ).
上的射影恰好为椭圆的右焦点,则该二面角的大小为( ).
| A.75° | B.60° | C.45° | D.30° |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=AD=1,AB=2,点E是AB上一点,当二面角P-EC-D的平面角为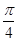 时,AE=( )
时,AE=( )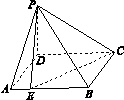
| A.1 | B. | C.2-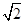 | D.2-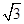 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com