
已知函数
(1)求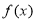 的最小正周期
的最小正周期
(2)在 中,
中,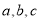 分别是
分别是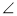 A、
A、 B、
B、 C的对边,若
C的对边,若 ,
, ,
,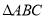 的面积为
的面积为 ,求
,求 的值
的值
【解析】
(1)f(x)=2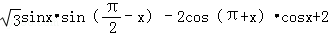
=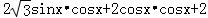 =
=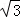 sin2x+(1+cos2x)+2
sin2x+(1+cos2x)+2
=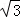 sin2x+cos2x)+3=2sin(2x+
sin2x+cos2x)+3=2sin(2x+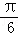 )+3∴T=
)+3∴T=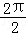 =π.
=π.
(2)由f(A)=4得2sin(2A+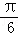 )+3=4,∴sin(2A+
)+3=4,∴sin(2A+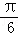 )=
)=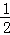 ,
,
又∵A为△ABC的内角,∴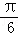 <2A+
<2A+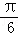 <
<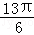 ,∴2A+
,∴2A+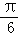 =
=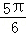 ,A=
,A=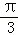 .
.
由S△ABC=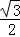 ,得
,得 bcsinA=
bcsinA= ×1×c×
×1×c×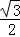 =
=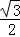 ,c=2.
,c=2.
由余弦定理得a2=b2+c2﹣2bccosA=1+4﹣2×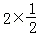 =3,∴a=
=3,∴a=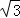 .
.
【解析】
试题分析:(1)根据诱导公式和二倍角公式、两角和的正弦公式对解析式化简,再由周期公式求f(x)的最小正周期;
(2)把条件代入f(x)的解析式化简,再由A的范围和正弦值求A,结合三角形面积公式条件和余弦定理求出边a.
考点:两角和与差的正弦函数;诱导公式的作用;三角函数的周期性及其求法; 解三角形.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源:2014-2015学年北京市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
在 中,“
中,“ ”是“
”是“ ”的( )
”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年安徽省淮北市高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
若函数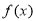 的导函数是
的导函数是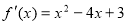 ,则函数
,则函数 (0<a<1)的单调递减区间是( )
(0<a<1)的单调递减区间是( )
A、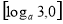 ,
,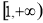
B、
C、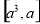
D、
查看答案和解析>>
科目:高中数学 来源:2014-2015学年天津市高三上学期第二次月考文科数学试卷(解析版) 题型:选择题
设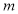 、
、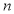 是两条不同的直线,
是两条不同的直线,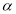 、
、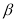 是两个不同的平面,则( )
是两个不同的平面,则( )
A.若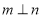 ,
,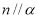 ,则
,则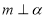
B.若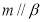 ,
,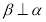 ,则
,则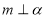
C.若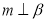 ,
,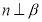 ,
,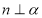 ,则
,则
D.若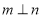 ,
, ,
,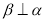 ,则
,则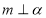
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:选择题
已知圆柱的底面半径为2,高为3,用一个与底面不平行的平面去截,若所截得的截面为椭圆,则椭圆的离心率的最大值为( )
A.1 B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com