练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系xOy中直线与抛物线C：交于A，B两点，且．

    求C的方程；

    若D为直线外一点，且的外心M在C上，求M的坐标．

    【答案】（1）（2）的坐标为或.

    【解析】

    （1）将直线方程与抛物线方程联立，设出A,B点坐标，根据韦达定理得x1x2和y1y2表达式，根据OA⊥OB可知x1x2+y1y2=0，即可求得p，从而得抛物线方程．（2）三角形的外心为中垂线的交点，利用中点坐标公式得线段AB中点N的坐标，得到线段的中垂线方程，将中垂线方程与抛物线方程联立即可得到外心M.

    （1）联立得， 设A(

    则，.

    从而.

    ，，

    即，解得.故的方程为.

    （2）设线段的中点为.

    由（1）知，，.

    则线段的中垂线方程为，即.

    联立得，解得或4.

    从而的外心的坐标为或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

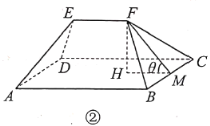
    【题目】市实施全域旅游，将乡村旅游公路建设与特色田园乡村发展结合，精心打造全长365公里的“1号公路”，对内串联区域内主要景区景点和自然村，对外通达周边县（市），以路引景、为景串线，形成一个“大环小圈、内连外引”的路网体系.如今的“1号公路”，不仅成为该市旅游业的“颜值担当”，更成为推动乡村振兴的“实力担当”，农村居住环境日益改善，新农村别墅随处可见.图①是一栋新农村别墅，它由上部屋顶和下部主体两部分组成.如图②，屋顶由四坡屋面构成，其中前后两坡屋面和是全等的等腰梯形，左右两坡屋面和是全等的三角形.点在平面和上的射影分别为（即：平面，垂足为；，垂足为）.已知，梯形的面积是面积的2.2倍..

    （1）当时，求屋顶面积的大小；

    （2）求屋顶面积关于的函数关系式；

    （3）已知上部屋顶造价与屋顶面积成正比，比例系数为（为正的常数），下部主体造价与其高度成正比，比例系数为.现欲造一栋上、下总高度为的别墅，试问：当为何值时，总造价最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=log4（4x+1）+kx与g（x）=log4（a2x﹣a），其中f（x）是偶函数．

    （1）求实数k的值；

    （2）求函数g（x）的定义域；

    (3)若函数f（x）与g（x）的图象有且只有一个公共点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆中心在原点，焦点在坐标轴上，直线与椭圆在第一象限内的交点是，点在轴上的射影恰好是椭圆的右焦点，椭圆另一个焦点是，且.

    （1）求椭圆的方程；

    （2）直线过点，且与椭圆交于两点，求的内切圆面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中表示不超过的最大整数，下列关于说法正确的有:______．

    ①的值域为[-1,1]

    ②为奇函数

    ③为周期函数，且最小正周期T=4

    ④在[0，2）上为单调增函数

    ⑤与的图像有且仅有两个公共点

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若是偶函数，求的值；

    （2）设函数，当时，有且只有一个实数根，求的取值范围；

    （3）若关于的方程在区间上有两个不相等的实数根，，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正三角形的边长为,将它沿高翻折,使点与点间的距离为,此时四面体外接球表面积为

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知下列命题：

    ①在线性回归模型中，相关指数越接近于1，表示回归效果越好；

    ②两个变量相关性越强，则相关系数r就越接近于1；

    ③在回归直线方程中，当解释变量每增加一个单位时，预报变量平均减少0.5个单位；

    ④两个模型中残差平方和越小的模型拟合的效果越好.

    ⑤回归直线恒过样本点的中心，且至少过一个样本点；

    ⑥若的观测值满足≥6.635，我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病；

    ⑦从统计量中得知有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推断出现错误． 其中正确命题的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝，其中a为常数．

    （1）当a＝1时，求f（x）的最大值；

    （2）若f（x）在区间(0，e]上的最大值为－2，求a的值．

    查看答案和解析>>

    同步练习册答案