
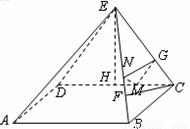
如图,四棱锥 ,底面
,底面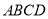 是矩形,平面
是矩形,平面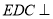 底面
底面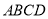 ,
,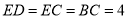 ,
,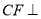 平面
平面 ,且点
,且点 在
在 上.
上.
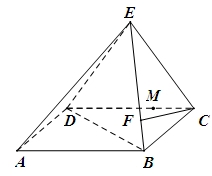
(1)求证: ;
;
(2)求三棱锥 的体积;
的体积;
(3)设点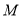 在线段
在线段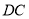 上,且满足
上,且满足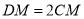 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得 平面
平面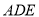 .
.
(1)证明见解析;(2)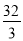 ;(3)存在点
;(3)存在点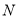 ,理由见解析.
,理由见解析.
【解析】
试题分析:﹙1﹚转化为证明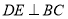 、
、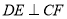 .其中
.其中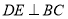 可转化为证明
可转化为证明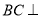 平面
平面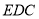 ,这由已知两个平面垂直可得到,而
,这由已知两个平面垂直可得到,而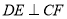 可由条件
可由条件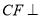 平面
平面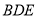 得到.﹙2﹚棱锥
得到.﹙2﹚棱锥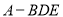 的体积转化为以
的体积转化为以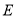 为顶点,以
为顶点,以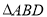 为底面的三棱锥;(3)过点
为底面的三棱锥;(3)过点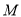 作
作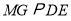 交
交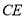 于
于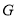 ,过
,过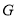 作
作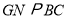 交
交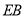 于
于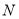 ,连接
,连接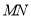 .然后证明
.然后证明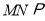 平面
平面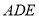 ,由此可确定
,由此可确定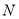 在
在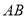 上的位置.
上的位置.
试题解析:(1)证明:∵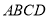 是矩形,∴
是矩形,∴ 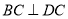 .
.
∵平面 平面
平面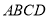 ,∴
,∴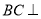 平面
平面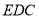 ,∴
,∴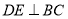 .
.
∵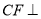 平面
平面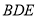 ,∴
,∴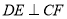 .
.
∵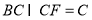 ,
,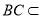 平面
平面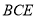 ,
,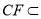 平面
平面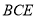 ,
,
∴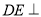 平面
平面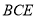 .
.
(2)过点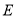 作
作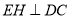 ,
,
∵平面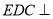 平面
平面 ,∴
,∴ 平面
平面 .
.
∵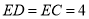 ,
,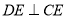 ,∴
,∴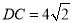 ,∴
,∴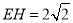 ,
,
∴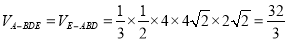 .
.
(3)过点 作
作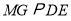 交
交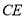 于
于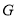 ,过
,过 作
作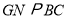 交
交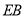 于
于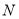 ,连接
,连接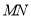 .
.
∵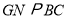 ,
,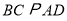 ,∴
,∴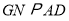 .
.
∵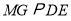 ,
,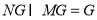 ,
,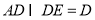 ,∴平面
,∴平面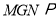 平面
平面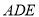 .
.
∵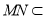 平面
平面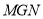 ,∴
,∴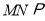 平面
平面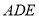 ,
,
∴线段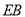 上存在点
上存在点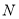 ,当
,当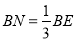 时,使得
时,使得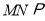 平面
平面 .
.
考点:1、直线、平面间的垂直关系;2、直线、平面间的平行关系;3、三棱锥的体积.


科目:高中数学 来源:2016届辽宁东北育才学校等三校高一下学期期末联考数学试卷(解析版) 题型:选择题
某时段内共有100辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60km/h的汽车数量为( )
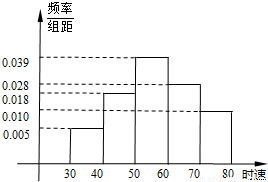
A.38辆 B.28辆 C.10辆 D.5辆
查看答案和解析>>
科目:高中数学 来源:2016届福建省龙岩市高一上学期教学质量检查数学试卷(解析版) 题型:填空题
如图是从上下底面处在水平状态下的棱长为 的正方体
的正方体 中分离出来的.
中分离出来的.

有如下结论:
① 在图中的度数和它表示的角的真实度数都是
在图中的度数和它表示的角的真实度数都是 ;
;
② ;
;
③ 与
与 所成的角是
所成的角是 ;
;
④若 ,则用图示中这样一个装置盛水,最多能盛
,则用图示中这样一个装置盛水,最多能盛 的水.
的水.
其中正确的结论是 (请填上你所有认为正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com