
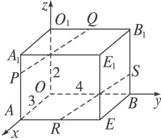
求证:PQ∥RS.
分析:利用向量证明PQ∥RS,只需建立适当的坐标系,表示出![]() ,
,![]() 的坐标,然后利用共线向量定理判定向量共线,从而得到直线平行.
的坐标,然后利用共线向量定理判定向量共线,从而得到直线平行.
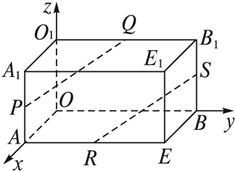
证明:如图,建立空间直角坐标系O—xyz.
则A(3,0,0),B(0,4,0),O1(0,0,2),A1(3,0,2),B1(0,4,2).
因为|PA|=2|PA1|,|SB1|=2|BS|,Q,R分别是棱O1B1,AE的中点,所以P(3,0,![]() ),Q(0,2,2,),R(3,2,0),S(0,4,
),Q(0,2,2,),R(3,2,0),S(0,4,![]() ).
).
所以![]() =(-3,2,
=(-3,2,![]() )=
)=![]() .
.
所以![]() ∥
∥![]() .
.
因为R![]() PQ,所以PQ∥RS.
PQ,所以PQ∥RS.
点拨:利用向量坐标运算证明线线平行时,(1)需证明两向量共线;(2)证明其中一个向量所在直线上一点不在另一个向量所在的直线上.


科目:高中数学 来源: 题型:
 如图在长方体ABCD-A1B1C1D1中,AB=AA1=2,BC=1,点E、F、G分别是AA1、AB、DD1的中点.
如图在长方体ABCD-A1B1C1D1中,AB=AA1=2,BC=1,点E、F、G分别是AA1、AB、DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com