
 元,而售出x件这种商品时,每件的价格为p元,这里
元,而售出x件这种商品时,每件的价格为p元,这里 (a,b是常数)。
(a,b是常数)。科目:高中数学 来源:不详 题型:解答题
 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0). 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (x-1)2.若存在,求出a,b,c的值;若不存在,请说
(x-1)2.若存在,求出a,b,c的值;若不存在,请说 [f(x1)+f(x2)]成立。
[f(x1)+f(x2)]成立。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
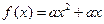 和
和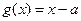 .其中
.其中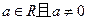 .
. 若函数
若函数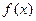 与
与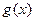 的图像的一个公共点恰好在x轴上,求
的图像的一个公共点恰好在x轴上,求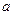 的值;w
的值;w 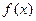 与
与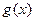 图像相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的
图像相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的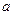 的值;如果没有,请说明理由.
的值;如果没有,请说明理由.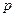 和
和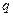 是方程
是方程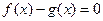 的两根,且满足
的两根,且满足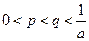 ,
,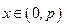 时,
时,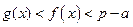 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com