
【题目】已知双曲线![]() 右支上的一点
右支上的一点![]() ,经过点
,经过点![]() 的直线与双曲线
的直线与双曲线![]() 的两条渐近线分别相交于
的两条渐近线分别相交于![]() ,
,![]() 两点.若点
两点.若点![]() ,
,![]() 分别位于第一,四象限,
分别位于第一,四象限,![]() 为坐标原点.当
为坐标原点.当![]() 时,
时,![]() 为( )
为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额如下表:
商店名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图,观察散点图,说明两个变量是否线性相关;
(2)用最小二乘法计算利润额y对销售额x的线性回归方程;
(3)当销售额为4千万元时,估计利润额的大小.
(参考公式: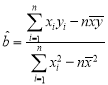 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 内有一点
内有一点![]() ,
,![]() 为圆
为圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线与
的垂直平分线与![]() 的连线交于点
的连线交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程.
的轨迹方程.
(Ⅱ)若动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 、
、![]() 两点,且以
两点,且以![]() 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点![]() .问是否存在一个定圆与动直线
.问是否存在一个定圆与动直线![]() 总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)写出函数![]() 的单调递减区间(无需证明) ;
的单调递减区间(无需证明) ;
(Ⅲ)若实数![]() 满足
满足![]() ,则称
,则称![]() 为
为![]() 的二阶不动点,求函数
的二阶不动点,求函数![]() 的二阶不动点的个数.
的二阶不动点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月16日下午5时左右,今年第22号台风“山竹”在广东江门川岛镇附近正面登陆,给当地人民造成了巨大的财产损失,某记者调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,并作出如下频率分布直方图.
五组,并作出如下频率分布直方图.
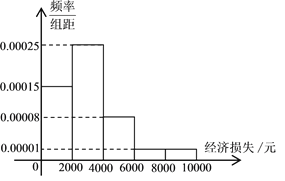
(Ⅰ)根据频率分布直方图估计该小区居民由于台风造成的经济损失的众数和平均值.
(Ⅱ)“一方有难,八方支援”,台风后居委会号召小区居民为台风重灾区捐款,![]() 记者调查的100户居民捐款情况如下表格,在如图表格空白处填写正确数字,并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
记者调查的100户居民捐款情况如下表格,在如图表格空白处填写正确数字,并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
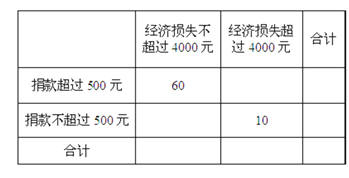
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查观众对某热播电视剧的喜爱程度,某电视台在甲、乙两地各随机抽取了8名观众作问卷调查,得分统计结果如图所示:
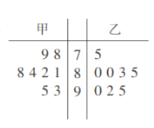
(1)计算甲、乙两地被抽取的观众问卷的平均得分;
(2)计算甲、乙两地被抽取的观众问卷得分的方差;
(3)若从甲地被抽取的8名观众中再邀请2名进行深入调研,求这2名观众中恰有1人的问卷调查成绩在90分以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 在倾斜角为
在倾斜角为![]() 的直线
的直线![]() 上,以坐标原点
上,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的方程为
的方程为![]() .
.
(1)写出![]() 的参数方程及
的参数方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com