
规定函数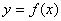 图象上的点到坐标原点距离的最小值叫做函数
图象上的点到坐标原点距离的最小值叫做函数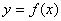 的“中心距离”,给出以下四个命题:
的“中心距离”,给出以下四个命题:
①函数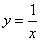 的“中心距离”大于1;
的“中心距离”大于1;
②函数 的“中心距离”大于1;
的“中心距离”大于1;
③若函数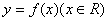 与
与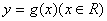 的“中心距离” 相等,则函数
的“中心距离” 相等,则函数 至少有一个零点.
至少有一个零点.
以上命题是真命题的是:
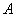 .①②
.①② 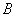 .②③
.②③ 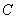 .①③
.①③ 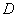 .①
.①
科目:高中数学 来源: 题型:
已知三条直线:l1:2x-y+a=0(a>0);l2:-4x+2y+ 1=0;l3:x+y-1=0,且l1与l2间的距离是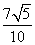 .
.
(1)求a的值;
(2)能否找到一点P,使P同时满足下列三个条件:
①点P在第一象限;
②点P到l1的距离是点P到l2的距离的 ;
;
③点P到l1的距离与点P到l3的距离之比是 ∶
∶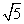 .若能,求点P的坐标;若不能,说明理由.
.若能,求点P的坐标;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设全集U=R,集合A={x|x>0},B={x|x>l},则集合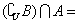
A.{x|0≤x <1} B.{x|0 <x≤1}
C.{x|x <0} D.{x|x >1}
查看答案和解析>>
科目:高中数学 来源: 题型:
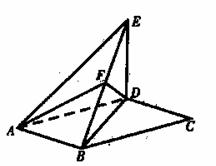
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4;将
△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD。
(1)求证:AB⊥DE;
(2)若点F为BE的中点,求直线AF与平面ADE所成角正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知三条直线:l1:2x-y+a=0(a>0);l2:-4x+2y+ 1=0;l3:x+y-1=0,且l1与l2间的距离是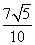 .
.
(1)求a的值;
(2)能否找到一点P,使P同时满足下列三个条件:
①点P在第一象限;
②点P到l1的距离是点P到l2的距离的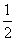 ;
;
③点P到l1的距离与点P到l3的距离之比是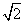 ∶
∶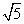 .若能,求点P的坐标;若不能,说明理由.
.若能,求点P的坐标;若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com