
 .
. )=1-P(F)=
)=1-P(F)= .
.
 。
。 ,满足条件的事件是甲、乙两人同时参加A岗位服务有
,满足条件的事件是甲、乙两人同时参加A岗位服务有 种结果,得到概率.
种结果,得到概率. ,满足条件的事件数是4个元素的全排列,得到概率.
,满足条件的事件数是4个元素的全排列,得到概率. =
= .
. .
. =
= .
. )=1-P(F)=
)=1-P(F)= .
. =
= .所以P(X=1)=1-P(X=2)=
.所以P(X=1)=1-P(X=2)= ,X的分布列为:
,X的分布列为:
 。
。

科目:高中数学 来源:不详 题型:解答题
 .
. 为在体操岗位服务的美国志愿者的个数,求
为在体操岗位服务的美国志愿者的个数,求 的分布列及期望
的分布列及期望查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
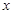 个红球与
个红球与 个白球(
个白球( ,且
,且 ),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。 ,求当
,求当 取得最大值时的
取得最大值时的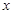 ,
, 的值;
的值; 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数 的期望
的期望 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 表示4名乘客在第4层下电梯的人数,则
表示4名乘客在第4层下电梯的人数,则 的数学期望为 ,方差为 .
的数学期望为 ,方差为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 和
和 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中: 的分布列与期望.
的分布列与期望.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com