
��5�֣���2012•����ģ�⣩�����ĸ������в���ȷ���ǣ� ��
A.������P�붨��A����4��0����B��4��0������PA��PB��б��֮��Ϊ��ֵ ����P�Ĺ켣Ϊ˫���ߵ�һ����
����P�Ĺ켣Ϊ˫���ߵ�һ����
B.��m��n��R������a��0���������㡰*����m*n=��m+n��2����m��n��2����x��0����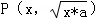 �Ĺ켣�������ߵ�һ����
�Ĺ켣�������ߵ�һ����
C.��֪��ԲA����x+1��2+y2=1��ԲB����x��1��2+y2=25����ԲM��ԲA���С���ԲB���У���Բ��Բ��M�Ĺ켣����Բ
D.��֪A��7��0����B����7��0����C��2����12������Բ��A��B��������CΪ��һ�����㣬����Բ����һ������Ĺ켣Ϊ˫����
D
��������
�������������ֱ�뷨����Aѡ���ж���P�Ĺ켣���̣������жϱ�ʾ�����ߣ������¶������㣬����ֱ�뷨��ѡ��B�����ߵĹ켣���̣������жϹ켣ͼ�Σ�����Բ��Բ��λ�ù�ϵ�����ö��巨�ж�ѡ��C�ж���Ĺ켣��������Բ���壬�ɶ��巨�ж�D�ж���Ĺ켣����
��������
A����P��x��y������Ϊֱ��PA��PB��б�ʴ��ڣ�����x�١�4��ֱ��PA��PB��б�ʷֱ���k1=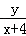 ��k2=
��k2=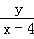 ����
����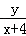 ��
��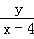 =
=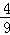 �������9y2=4x2��64��
�������9y2=4x2��64��
��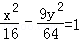 ��x�١�4�����ද��P�Ĺ켣Ϊ˫���ߵ�һ���֣�A��ȷ��
��x�١�4�����ද��P�Ĺ켣Ϊ˫���ߵ�һ���֣�A��ȷ��
B����m*n=��m+n��2����m��n��2����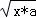 =
=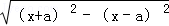 =
=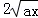 ����P��x��y������y=
����P��x��y������y=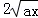 ����y2=4ax��x��0��y��0����������
����y2=4ax��x��0��y��0����������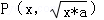 �Ĺ켣�������ߵ�һ���֣�B��ȷ��
�Ĺ켣�������ߵ�һ���֣�B��ȷ��
C���������֪����ԲM�붨ԲA�������붨ԲB������
��MA=r+1��MB=5��r
��MA+MB=6��AB=2
�දԲԲ��M�Ĺ켣����A��BΪ�������Բ��C��ȷ��
D�����Բ����һ���������D ��x��y����
����Բ��A��B���㣬�� CA+DA=CB+DB��
��15+DA=13+DB����DB��DA=2��AB��
����Բ����һ����Ĺ켣����A��BΪ�����˫����һ֧��D����
��ѡ D


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��[ͬ��]2014���˽�A��ѡ��һ1-2������4.2��ϰ���������棩 ���ͣ�ѡ����
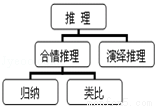
��ͼ�ǡ�������֪ʶ�ṹ��ͼ�����ݸÿ�ͼ�ɵ�
��1������������Ҫ��������������
��2��֪���������������ֻ�ܽ��С��������������ݵ�ѧϰ
��3�������ɡ��롰��ȡ���������������
��4��������ѧϰ����ȡ���ѧϰ�����ɡ�
��Щ���⣨ ��
A.����2���ⶼ��ȷ B.����3���ⶼ��ȷ C.��1����4����ȷ D.ȫ����ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014���˽�A��ѡ��һ1-2��һ��1.1��ϰ���������棩 ���ͣ�ѡ����
��2014•����һģ��ij�̳�Ϊ���˽�ë�µ���������y����������ƽ������x���棩֮��Ĺ�ϵ�����ͳ����ij4���µ����������뵱��ƽ�����£����������±���
��ƽ������x���棩 | 17 | 13 | 8 | 2 |
��������y������ | 24 | 33 | 40 | 55 |
�ɱ�������������Իع鷽��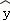 =bx+a�е�b=��2��������Ԥ���¸��µ�ƽ������ԼΪ6�棬�ݴ˹��Ƹ��̳��¸���ë��������ԼΪ�� ������
=bx+a�е�b=��2��������Ԥ���¸��µ�ƽ������ԼΪ6�棬�ݴ˹��Ƹ��̳��¸���ë��������ԼΪ�� ������
A.46 B.40 C.38 D.58
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014���˽�A��ѡ��2-1 �ڶ���Բ�����뷽����ϰ���������棩 ���ͣ������
��5�֣���2008•�ζ�����ģ����֪˫����x2��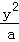 =1��һ����������ֱ��x��2y+3=0��ֱ����a= ��
=1��һ����������ֱ��x��2y+3=0��ֱ����a= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014���˽�A��ѡ��2-1 �ڶ���Բ�����뷽����ϰ���������棩 ���ͣ�ѡ����
��5�֣���2008•�㽭����˫����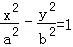 ���������㵽һ���ߵľ���֮��Ϊ3��2����˫���ߵ��������ǣ� ��
���������㵽һ���ߵľ���֮��Ϊ3��2����˫���ߵ��������ǣ� ��
A.3 B.5 C.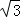 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014�˽�B��ѡ��4-5 2.4���ֵ����Сֵ �Ż���ѧģ�ͣ������棩 ���ͣ������
������a��b��c��d����ab+bc+cd+ad=1����ôa+b+c+d����Сֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014�˽�B��ѡ��4-5 2.4���ֵ����Сֵ �Ż���ѧģ�ͣ������棩 ���ͣ������
��x��y��R+����x2+3y2=1����x+3y�����ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016������ʡ��һ��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��֪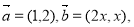
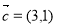 ����
����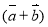 ��
��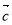 ����ʵ��x��ֵ��
����ʵ��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]�˽�B��ѡ��4-5 1.1����ʽ�����ʺ�һԪ���β���ʽ�Ľⷨ�������棩 ���ͣ�ѡ����
��2014•������ģ��������������ȷ���ǣ� ��
A.a��b��c��d⇒a��c��b��d B.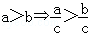
C.ac��bc⇒a��b D.ac2��bc2⇒a��b
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com