
(2014•江西一模)某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x(℃) | 17 | 13 | 8 | 2 |
月销售量y(件) | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程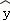 =bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
=bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
A.46 B.40 C.38 D.58
科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.2练习卷(解析版) 题型:选择题
如图所示,l1∥l2∥l3,下列比例式正确的是( )
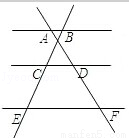
A.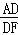 =
=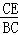 B.
B.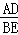 =
=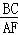 C.
C.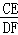 =
=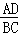 D.
D.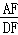 =
=
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.2练习卷(解析版) 题型:选择题
(2010•泰安二模)某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设H0:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出P(Χ2≥6.635)≈0.01,则下列说法正确的是( )
A.这种疫苗能起到预防甲型H1N1流感的有效率为1%
B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1
C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”
D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.2练习卷(解析版) 题型:选择题
(2014•抚州模拟)下列四个命题中
①设有一个回归方程y=2﹣3x,变量x增加一个单位时,y平均增加3个单位;
②命题P:“?x0∈R,x02﹣x0﹣1>0“的否定¬P:“?x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(﹣l<X<0)= ﹣p;
﹣p;
④在一个2×2列联表中,由计算得K2=6.679,则有99%的把握确认这两个变量间有关系.
其中正确的命题的个数有( )
附:本题可以参考独立性检验临界值表
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10. |
|
828 |
|
|
|
|
|
|
|
|
|
|
|
|
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•张掖一模)对具有线性相关关系的变量x,y有一组观测数据(xi,yi)( i=1,2,…,8),其回归直线方程是 =
=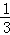 x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
A.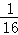 B.
B.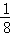 C.
C.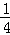 D.
D.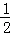
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•湖北)经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系,对每小组学生每周用于数学的学习时间x与数学成绩y进行数据收集如下:
x | 15 | 16 | 18 | 19 | 22 |
y | 102 | 98 | 115 | 115 | 120 |
由表中样本数据求得回归方程为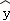 =kx+a,则点(a,b)与直线x+18y=100的位置关系是( )
=kx+a,则点(a,b)与直线x+18y=100的位置关系是( )
A.点在直线左侧 B.点在直线右侧 C.点在直线上 D.无法确定
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:解答题
(12分)(2008•崇文区一模)已知抛物线C:y=ax2,点P(1,﹣1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
(1)求抛物线C的焦点坐标;
(2)若点M满足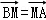 ,求点M的轨迹方程.
,求点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)(2012•安徽模拟)下列四个命题中不正确的是( )
A.若动点P与定点A(﹣4,0)、B(4,0)连线PA、PB的斜率之积为定值 ,则动点P的轨迹为双曲线的一部分
,则动点P的轨迹为双曲线的一部分
B.设m,n∈R,常数a>0,定义运算“*”:m*n=(m+n)2﹣(m﹣n)2,若x≥0,则动点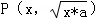 的轨迹是抛物线的一部分
的轨迹是抛物线的一部分
C.已知两圆A:(x+1)2+y2=1、圆B:(x﹣1)2+y2=25,动圆M与圆A外切、与圆B内切,则动圆的圆心M的轨迹是椭圆
D.已知A(7,0),B(﹣7,0),C(2,﹣12),椭圆过A,B两点且以C为其一个焦点,则椭圆的另一个焦点的轨迹为双曲线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com