
(12分)(2008•崇文区一模)已知抛物线C:y=ax2,点P(1,﹣1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
(1)求抛物线C的焦点坐标;
(2)若点M满足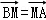 ,求点M的轨迹方程.
,求点M的轨迹方程.
(1)(0,﹣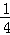 ).(2):x=﹣1(y≤﹣1且y≠﹣5).
).(2):x=﹣1(y≤﹣1且y≠﹣5).
【解析】
试题分析:(1)将P代入抛物线C的方程即可求得a,进而抛物线的方程可得.
(2)设直线PA的方程为y+1=k1(x﹣1),与抛物线方程联立消去y,得到关于x1的一元二次方程根据韦达定理求得x1与k1的关系,同样设直线PB的方程为y+1=k2(x﹣1)与抛物线方程联立消去y,进而可得x2与k2的关系,设点M的坐标为(x,y)根据向量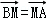 的关系求得x=﹣1,得出M的轨迹.
的关系求得x=﹣1,得出M的轨迹.
【解析】
(1)将P(1,﹣1)代入抛物线C的方程y=ax2得a=﹣1,
∴抛物线C的方程为y=﹣x2,即x2=﹣y.
焦点坐标为F(0,﹣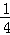 ).
).
(2)设直线PA的方程为y+1=k1(x﹣1),
联立方程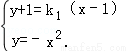 消去y得x2+k1x﹣k1﹣1=0,
消去y得x2+k1x﹣k1﹣1=0,
则1•x1=﹣k1﹣1,即x1=﹣k1﹣1.
由△=k12﹣4(﹣k1﹣1)=(k1+2)2>0,得k1≠﹣2.
同理直线PB的方程为y+1=k2(x﹣1),
联立方程 消去y得x2+k2x﹣k2﹣1=0,
消去y得x2+k2x﹣k2﹣1=0,
则1•x2=﹣k2﹣1,即x2=﹣k2﹣1.且k2≠﹣2.
又∵k1+k2=0,∴k1≠2.
设点M的坐标为(x,y),由

又∵k1+k2=0,∴x=﹣1.
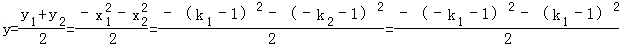
=﹣(k12+1)≤﹣1,
又k1≠±2,∴y≠﹣5.
∴所求M的轨迹方程为:x=﹣1(y≤﹣1且y≠﹣5).


科目:高中数学 来源: 题型:
| x2+ax+1 |
| A、(-2,2) |
| B、(-∞,-2)∪(2,+∞) |
| C、(-∞,-2]∪[2,+∞) |
| D、[-2,2] |
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.1练习卷(解析版) 题型:填空题
(2013•中山模拟)(几何证明选讲选做题)
如图,△ABC中,D、E分别在边AB、AC上,CD平分∠ACB,DE∥BC,如果AC=10,BC=15,那么AE= .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.2练习卷(解析版) 题型:选择题
(2014•永州三模)随机调查某校110名学生是否喜欢跳舞,由列联表和公式K2= 计算出K2,并由此作出结论:“有99%的可能性认为学生喜欢跳舞与性别有关”,则K2可以为( )
计算出K2,并由此作出结论:“有99%的可能性认为学生喜欢跳舞与性别有关”,则K2可以为( )
附表:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
A.3.565 B.4.204 C.5.233 D.6.842
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•江西一模)某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x(℃) | 17 | 13 | 8 | 2 |
月销售量y(件) | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程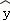 =bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
=bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
A.46 B.40 C.38 D.58
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•葫芦岛二模)已知x、y取值如下表:
x | 0 | 1 | 4 | 5 | 6 | 8 |
y | 1.3 | 1.8 | 5.6 | 6.1 | 7.4 | 9.3 |
从所得的散点图分析可知:y与x线性相关,且 =0.95x+a,则a=( )
=0.95x+a,则a=( )
A.1.30 B.1.45 C.1.65 D.1.80
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:填空题
(5分)(2008•嘉定区二模)已知双曲线x2﹣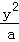 =1的一条渐近线与直线x﹣2y+3=0垂直,则a= .
=1的一条渐近线与直线x﹣2y+3=0垂直,则a= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)(2008•浙江)若双曲线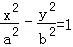 的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是( )
的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是( )
A.3 B.5 C.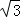 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com