
某学生对函数![]() 进行研究后,得出如下四个结论:
进行研究后,得出如下四个结论:
⑴函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
⑵存在常数![]() ,使
,使![]() 对一切实数x均成立;
对一切实数x均成立;
⑶点![]() 是函数
是函数![]() 图像的一个对称中心;
图像的一个对称中心;
⑷函数![]() 图像关于直线
图像关于直线![]() 对称.
对称.
其中正确的是 .(把你认为正确命题的序号都填上)
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年本溪县高三暑期补课阶段考试数学卷 题型:填空题
某学生对函数 进行研究后,得出如
进行研究后,得出如
下结论:
①函数 上单调递增;
上单调递增;
②存在常数M>0,使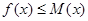 对一切实数x均成立;
对一切实数x均成立;
③函数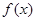 在(0,
在(0,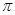 )上无最小值,但一定有最大值;
)上无最小值,但一定有最大值;
④点(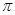 ,0)是函数
,0)是函数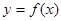 图象的一个对称中心
图象的一个对称中心
其中正确命题的序号是 。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年本溪县高三暑期补课阶段考试数学卷 题型:填空题
某学生对函数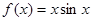 进行研究后,得出如
进行研究后,得出如
下结论:
①函数 上单调递增;
上单调递增;
②存在常数M>0,使 对一切实数x均成立;
对一切实数x均成立;
③函数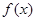 在(0,
在(0,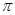 )上无最小值,但一定有最大值;
)上无最小值,但一定有最大值;
④点(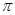 ,0)是函数
,0)是函数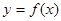 图象的一个对称中心
图象的一个对称中心
其中正确命题的序号是 。
查看答案和解析>>
科目:高中数学 来源: 题型:
某学生对函数![]() 进行研究后,得出如下四个结论:
进行研究后,得出如下四个结论:
⑴函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
⑵存在常数![]() ,使
,使![]() 对一切实数x均成立;
对一切实数x均成立;
⑶点![]() 是函数
是函数![]() 图像的一个对称中心;
图像的一个对称中心;
⑷函数![]() 图像关于直线
图像关于直线![]() 对称.
对称.
其中正确的是 .(把你认为正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com