Question

2．已知△ABC是腰长为2等腰直角三角形，D点是斜边AB的中点，点P在CD上，且$\overrightarrow{CP}=\frac{1}{2}\overrightarrow{PD}$，则$\overrightarrow{PA}•\overrightarrow{PB}$=（　　）

• A． -$\frac{3}{4}$
• B． -$\frac{10}{9}$
• C． 0
• D． 4

Answer 1

分析 以CB，CA两直线分别为x，y轴，建立坐标系，根据条件可求出C，A，B，D几点的坐标，设P（x，y），而根据$\overrightarrow{CP}=\frac{1}{2}\overrightarrow{PD}$即可求出点P的坐标，从而得出向量$\overrightarrow{PA}，\overrightarrow{PB}$的坐标，然后进行数量积的坐标运算即可．

解答 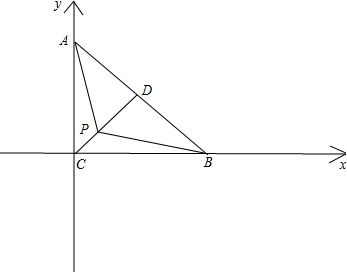解：如图，分别以边CB，CA所在直线为x，y轴，建立平面直角坐标系，则：
C（0，0），A（0，2），B（2，0），D（1，1）；
设P（x，y），∵$\overrightarrow{CP}=\frac{1}{2}\overrightarrow{PD}$；
（x，y）=$\frac{1}{2}$（1-x，1-y）；
∴$\left\{\begin{array}{l}{x=\frac{1}{2}（1-x）}\\{y=\frac{1}{2}（1-y）}\end{array}\right.$；
解得$x=y=\frac{1}{3}$；
∴$P（\frac{1}{3}，\frac{1}{3}）$，$\overrightarrow{PA}=（-\frac{1}{3}，\frac{5}{3}）$，$\overrightarrow{PB}=（\frac{5}{3}，-\frac{1}{3}）$；
∴$\overrightarrow{PA}•\overrightarrow{PB}=-\frac{10}{9}$．
故选B．

点评 考查建立平面直角坐标系，利用向量坐标求数量积的方法，由点的坐标可求向量的坐标，向量坐标的数乘、数量积的运算．