
【题目】已知函数![]() .
.
(1)设![]() ,试讨论
,试讨论![]() 单调性;
单调性;
(2)设![]() ,当
,当![]() 时,任意
时,任意![]() ,存在
,存在![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 和
和![]() 上是减函数;当
上是减函数;当![]() 时,
时,![]() 在
在![]() 上是减函数;当
上是减函数;当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 和
和![]() 上是减函数;(2)
上是减函数;(2)![]() .
.
【解析】
试题(1)先求出![]() 的导数,
的导数,![]() ,然后在
,然后在![]() 的范围内讨论
的范围内讨论![]() 的大小以确定
的大小以确定![]() 和
和![]() 的解集;(2)
的解集;(2)![]() 时,代入结合上问可知函数
时,代入结合上问可知函数![]() 在在
在在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,即在
上是增函数,即在![]() 取最小值,若
取最小值,若![]() ,存在
,存在![]() ,使
,使![]() ,即存在
,即存在![]() 使得
使得![]() .从而得出实数
.从而得出实数![]() 的取值范围.注意
的取值范围.注意![]() 不能用基本不等式,因为
不能用基本不等式,因为![]() 等号取不到,实际上
等号取不到,实际上![]() 为减函数.所以其值域为
为减函数.所以其值域为![]() ,从而
,从而![]() ,即有
,即有![]() .
.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
令![]() ,可得
,可得![]() ,
,![]() ,
,![]() 2分
2分
①当![]() 时,由
时,由![]() 可得
可得![]() ,故此时函数
,故此时函数![]() 在
在![]() 上是增函数.
上是增函数.
同样可得![]() 在
在![]() 和
和![]() 上是减函数. 4分
上是减函数. 4分
②当![]() 时,
时,![]() 恒成立,故此时函数
恒成立,故此时函数![]() 在
在![]() 上是减函数. 6分
上是减函数. 6分
③当![]() 时,由
时,由![]() 可得
可得![]() ,故此时函数
,故此时函数![]() 在
在![]() 上是增函数,
上是增函数,
在![]() 和
和![]() 上是减函数; 8分
上是减函数; 8分
(2)当![]() 时,由(1)可知
时,由(1)可知![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
所以对任意的![]() ,有
,有![]() ,
,
由条件存在![]() ,使
,使![]() ,所以
,所以![]() , 12分
, 12分
即存在![]() ,使得
,使得![]() ,
,
即![]() 在
在![]() 时有解,
时有解,
亦即![]() 在
在![]() 时有解,
时有解,
由于![]() 为减函数,故其值域为
为减函数,故其值域为![]() ,
,
从而![]() ,即有
,即有![]() ,所以实数
,所以实数![]() 的取值范围是
的取值范围是![]() . 16分
. 16分


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某学校为了解高三复习效果,从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩,分成6组制成频率分布直方图如图所示:
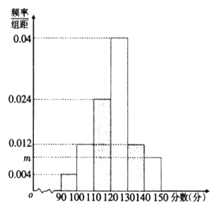
(1)求![]() 的值;并且计算这50名同学数学成绩的样本平均数
的值;并且计算这50名同学数学成绩的样本平均数![]() ;
;
(2)该学校为制定下阶段的复习计划,从成绩在![]() 的同学中选出3位作为代表进行座谈,记成绩在
的同学中选出3位作为代表进行座谈,记成绩在![]() 的同学人数位
的同学人数位![]() ,写出
,写出![]() 的分布列,并求出期望.
的分布列,并求出期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() 六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中
六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中![]() ,各踢了
,各踢了![]() 场,
场, ![]() 各踢了
各踢了![]() 场,
场, ![]() 踢了
踢了![]() 场,且
场,且![]() 队与
队与![]() 队未踢过,
队未踢过, ![]() 队与
队与![]() 队也未踢过,则在第一周的比赛中,
队也未踢过,则在第一周的比赛中, ![]() 队踢的比赛的场数是( )
队踢的比赛的场数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 为常数).
为常数).
(1)若函数![]() 与函数
与函数![]() 在
在![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,证明:
,证明: ![]() ;
;
(3)若对任意![]() ,不等式恒
,不等式恒![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com