
【题目】如图所示,![]() 是正三角形,线段
是正三角形,线段![]() 和
和![]() 都垂直于平面
都垂直于平面![]() ,设
,设![]() ,
,![]() ,且
,且![]() 为
为![]() 的中点.
的中点.
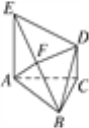
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成的较小二面角的大小.
所成的较小二面角的大小.
【答案】(1)见证明(2)见证明![]()
【解析】
(1)利用三角形的中位线定理、平行四边形的判定和性质定理、线面平行的判定定理即可证明;(2)利用线面、面面垂直的判定和性质定理即可证明;(3)延长ED交AC延长线于G′,连BG′,只要证明BG′⊥平面ABE即可得到∠ABE为所求的平面BDE与平面ABC所成二面角,在等腰直角三角形ABE中即可得到.
(1)如图所示,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .
.

∵![]() ,
,![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() .
.
∴四边形![]() 为平行四边形.
为平行四边形.
故![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)∵![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() 是正三角形,∴
是正三角形,∴![]() .
.
∴![]() 平面
平面![]() .
.
又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∴平面![]() 平面
平面![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
(3)延长![]() 交
交![]() 的延长线于
的延长线于![]() ,连
,连![]() .
.
由![]() ,
,![]() 知,
知,![]() 为
为![]() 的中点,
的中点,
又![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
又![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
∴![]() 为所求二面角的平面角.
为所求二面角的平面角.
在等腰直角三角形![]() 中,易求
中,易求![]() .
.
故所求二面角的大小为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】有一名同学家开了一个小卖部,他为了研究气温对某种引领销售的影响,记录了2015年7月至12月每月15号下午14时的气温和当天的饮料杯数,得到如下资料:

该同学确定的研究方案是:现从这六组数据中选取2组,用剩下的4组数据取线性回归方程,再用被选中的2组数据进行检验.
(1)求选取2组数据恰好是相邻两个月的概率;
(2)若选中的是8月与12月的两组数据,根据剩下的4组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若有线性回归方程得到估计,数据与所宣称的检验数据的误差不超过3杯,则认为得到的线性回归方程是理想的,请问(2)所得线性回归方程是否理想.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: 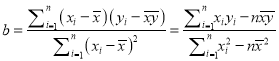 ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆内画1条线段,将圆分割成两部分;画2条相交线段,彼此分割成4条线段,将圆分割成4部分;画3条线段,彼此最多分割成9条线段,将圆最多分割成7部分;画4条线段,彼此最多分割成16条线段,将圆最多分割成11部分.那么




(1)在圆内画5条线段,它们彼此最多分割成多少条线段?将圆最多分割成多少部分?
(2)猜想:圆内两两相交的n条线段,彼此最多分割成多少条线段?
(3)猜想:在圆内画n条线段,两两相交,将圆最多分割成多少部分?
并用数学归纳法证明你所得到的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
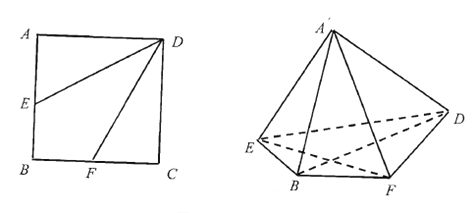
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,将
的中点,将![]() ,
, ![]() ,分别沿
,分别沿![]() ,
, ![]() 折起,使
折起,使![]() ,
, ![]() 两点重合于点
两点重合于点![]() ,连接
,连接![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣3x
(1)若不等式f(x)≥m对任意x∈[0,1]恒成立,求实数![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,当m取最大值时,设x>0,y>0且2x+4y+m=0,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com