
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,将
的中点,将![]() ,
, ![]() ,分别沿
,分别沿![]() ,
, ![]() 折起,使
折起,使![]() ,
, ![]() 两点重合于点
两点重合于点![]() ,连接
,连接![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
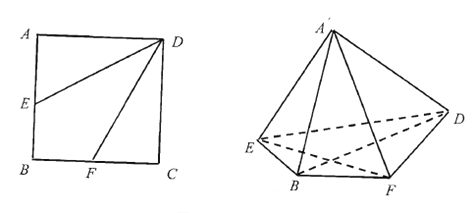
【答案】(1)见解析(2)![]()
【解析】试题分析:(Ⅰ) ![]() ,
, ![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
, ![]() ,由已知可得
,由已知可得![]() ,
, ![]() 平面
平面![]() ;(Ⅱ)由面面垂直的性质定理可得
;(Ⅱ)由面面垂直的性质定理可得![]() 为
为![]() 与平面
与平面![]() 所成角,在
所成角,在![]() △
△![]() 中,
中, ![]() ,从而可得
,从而可得![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
试题解析:(Ⅰ) ![]() ,
, ![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
, ![]() ,
,
由已知可得![]() ,
, ![]() 平面
平面![]() ;
;
(Ⅱ)由(Ⅰ)知平面![]() 平面
平面![]() ,则
,则![]() 为
为![]() 与平面
与平面![]() 所成角,
所成角,
设![]() ,
, ![]() 交于点
交于点![]() ,连
,连![]() ,则
,则![]() ,
, ![]() ,
,
又![]() 平面
平面![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() ,
,
在![]() △
△![]() 中,
中, ![]() ,
,
![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【方法点晴】本题主要考查线面垂直的判定定理及线面角的求法,属于难题. 证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】现有![]() 六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中
六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中![]() ,各踢了
,各踢了![]() 场,
场, ![]() 各踢了
各踢了![]() 场,
场, ![]() 踢了
踢了![]() 场,且
场,且![]() 队与
队与![]() 队未踢过,
队未踢过, ![]() 队与
队与![]() 队也未踢过,则在第一周的比赛中,
队也未踢过,则在第一周的比赛中, ![]() 队踢的比赛的场数是( )
队踢的比赛的场数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2018·赣中联考]李冶(1192-1279),真实栾城(今属河北石家庄市)人,金元时期的数学家、诗人,晚年在封龙山隐居讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径、正方形的边长等.其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为13.75亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:240平方步为1亩,圆周率按3近似计算)( )
A. 10步,50步 B. 20步,60步 C. 30步,70步 D. 40步,80步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:不等式![]() 的解集中的整数有且仅有-1,0,1.求a的取值范围.
的解集中的整数有且仅有-1,0,1.求a的取值范围.
命题Q:集合![]() 且
且![]() .
.
(1)分别求命题P、Q为真命题时的实数a的取值范围;
(2)当实数a取何值时,命题P、Q中有且仅有一个为真命题;
(3)设P、Q皆为真时a的取值范围为集合S,![]() ,若全集
,若全集![]() ,
,![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com