
【题目】设函数![]() ,
, ![]() 为曲线
为曲线![]() 在点
在点![]() 处的切线.
处的切线.
(Ⅰ)求![]() 的方程.
的方程.
(Ⅱ)当![]() 时,证明:除切点
时,证明:除切点![]() 之外,曲线
之外,曲线![]() 在直线
在直线![]() 的下方.
的下方.
(Ⅲ)设![]() ,
, ![]() ,
, ![]() ,且满足
,且满足![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() (Ⅱ)见解析(Ⅲ)
(Ⅱ)见解析(Ⅲ)![]() .
.
【解析】试题分析:(Ⅰ)先求导,再求![]() 的值,根据导数的几何意义可知切线的斜率即为
的值,根据导数的几何意义可知切线的斜率即为![]() .由点斜式可得直线方程.(Ⅱ)即证明
.由点斜式可得直线方程.(Ⅱ)即证明![]() ,
, ![]() 恒成立.变形可得即证
恒成立.变形可得即证![]() 恒成立即可.令
恒成立即可.令![]() 求导,讨论导数的正负,根据导数的正负可得函数
求导,讨论导数的正负,根据导数的正负可得函数![]() 的单调性.根据单调性可求其最值,其最大值小于0即可.(Ⅲ)当
的单调性.根据单调性可求其最值,其最大值小于0即可.(Ⅲ)当![]() 且
且![]() 时由(Ⅱ)可知
时由(Ⅱ)可知![]() .当
.当![]() 中至少有一个大于等于
中至少有一个大于等于![]() 时,可用配方法求各自值域再相加.
时,可用配方法求各自值域再相加.
试题解析:解:(Ⅰ) 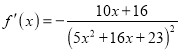 .
.
所以![]() .
.
所以 L的方程为![]() ,即
,即![]() . 3分
. 3分
(Ⅱ)要证除切点![]() 之外,曲线C在直线L的下方,只需证明
之外,曲线C在直线L的下方,只需证明![]() ,
, ![]() 恒成立.
恒成立.
因为![]() ,
,
所以只需证明![]() ,
, ![]() 恒成立即可. 5分
恒成立即可. 5分
设![]()
则![]() .
.
令![]() ,解得
,解得![]() ,
, ![]() . 6分
. 6分
当![]() 在
在![]() 上变化时,
上变化时, ![]() 的变化情况如下表
的变化情况如下表

所以![]() ,
, ![]() 恒成立. 8分
恒成立. 8分
(Ⅲ)(ⅰ)当![]() 且
且![]() 时,
时,
由(Ⅱ)可知: ![]() ,
,
![]() ,
, ![]() .
.
三式相加,得![]() .
.
因为![]() ,
,
所以![]() ,且当
,且当![]() 时取等号. 11分
时取等号. 11分
(ⅱ)当![]() 中至少有一个大于等于
中至少有一个大于等于![]() 时,
时,
不妨设![]() ,则
,则![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() .
.
综上所述,当![]() 时
时![]() 取到最大值
取到最大值![]() . 14分
. 14分


科目:高中数学 来源: 题型:
【题目】现有![]() 六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中
六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中![]() ,各踢了
,各踢了![]() 场,
场, ![]() 各踢了
各踢了![]() 场,
场, ![]() 踢了
踢了![]() 场,且
场,且![]() 队与
队与![]() 队未踢过,
队未踢过, ![]() 队与
队与![]() 队也未踢过,则在第一周的比赛中,
队也未踢过,则在第一周的比赛中, ![]() 队踢的比赛的场数是( )
队踢的比赛的场数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的渐近线方程是
的渐近线方程是![]() ,右焦点
,右焦点![]() ,则双曲线
,则双曲线![]() 的方程为_________,又若点
的方程为_________,又若点![]() ,
, ![]() 是双曲线
是双曲线![]() 的左支上一点,则
的左支上一点,则![]() 周长的最小值为__________.
周长的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2018·赣中联考]李冶(1192-1279),真实栾城(今属河北石家庄市)人,金元时期的数学家、诗人,晚年在封龙山隐居讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径、正方形的边长等.其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为13.75亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:240平方步为1亩,圆周率按3近似计算)( )
A. 10步,50步 B. 20步,60步 C. 30步,70步 D. 40步,80步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 为常数).
为常数).
(1)若函数![]() 与函数
与函数![]() 在
在![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,证明:
,证明: ![]() ;
;
(3)若对任意![]() ,不等式恒
,不等式恒![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数中,表示同一个函数的是( ).
A.y=x+1和y=![]() B.y=x0和y=
B.y=x0和y=![]() C.f(x)=(x-1)2和g(x)=(x+1)2D.f(x)=
C.f(x)=(x-1)2和g(x)=(x+1)2D.f(x)=![]() 和g(x)=
和g(x)=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com