
【题目】设函数![]() ,其中
,其中![]() 为正实数.
为正实数.
(1)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,证明
时,证明![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)讨论研究函数![]() 的单调性,求出函数
的单调性,求出函数![]() 在
在![]() 上的最大值.要不等式
上的最大值.要不等式![]() 恒成立,只需最大值小于零,即可求出.
恒成立,只需最大值小于零,即可求出.
(2)将原不等式等价变形为![]() ,由(1)可知
,由(1)可知![]() ,试证
,试证![]() 在
在![]() 时恒成立,即可由不等式性质证出
时恒成立,即可由不等式性质证出![]() .
.
(1)由题意得![]()
设![]() ,则
,则![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,![]() ,满足题意;
,满足题意;
②当![]() 时,即
时,即![]() 时,则
时,则![]() 的图象的对称轴
的图象的对称轴![]()
因为![]() ,
,
所以![]() 在
在![]() 上存在唯一实根,设为
上存在唯一实根,设为![]() ,则当
,则当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
此时![]() ,不合题意.
,不合题意.
综上可得,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)![]() 等价于
等价于![]()
因为![]() ,所以
,所以![]() ,所以原不等式等价于
,所以原不等式等价于![]() ,
,
由(1)知当![]() 时,
时,![]() 在
在![]() 上恒成立,整理得
上恒成立,整理得![]()
令![]() ,则
,则 ,
,
所以函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
所以,当![]() 时,恒有
时,恒有![]() ,
,


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
![]()
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:

(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
(3)若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为![]() ,求
,求![]() 的数学期望与方差.
的数学期望与方差.
参考公式:
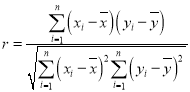 ,
,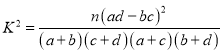 ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相交.
线性相交.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() :
:![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为16(
的面积为16(![]() 为坐标原点).
为坐标原点).
(1)求![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的焦点
的焦点![]() 且
且![]() 不与
不与![]() 轴垂直,与
轴垂直,与![]() 交于
交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现计划用两张铁丝网在一片空地上围成一个梯形养鸡场![]() ,
,![]() ,
,![]() ,已知
,已知![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成,
的铁丝网折成,![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成.设上底
的铁丝网折成.设上底![]() 的长为
的长为![]() ,所围成的梯形面积为
,所围成的梯形面积为![]() .
.
(1)求S关于x的函数解析式,并求x的取值范围;
(2)当x为何值时,养鸡场的面积最大?最大面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为等边三角形,其中O为BC中点,且
为等边三角形,其中O为BC中点,且![]() .
.
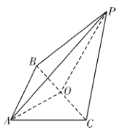
(1)求证:平面![]() 平面PBC;
平面PBC;
(2)若![]() 且
且![]() 平面EBC,其中E为AP上的点,求CE与平面ABC所成角的正弦值.
平面EBC,其中E为AP上的点,求CE与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
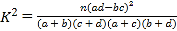 (其中
(其中![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com