练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知过点A(0，1)且斜率为k的直线l与圆C：(x－2)2＋(y－3)2＝1交于M，N两点．

    (1)求k的取值范围；

    (2)若＝12，其中O为坐标原点，求|MN|.

    【答案】见解析

    【解析】

    解：(1)由题设可知直线l的方程为y＝kx＋1.

    因为直线l与圆C交于两点，所以<1，

    解得<k<.

    所以k的取值范围为.

    (2)设M(x1，y1)，N(x2，y2)．

    将y＝kx＋1代入方程(x－2)2＋(y－3)2＝1，

    整理得(1＋k2)x2－4(1＋k)x＋7＝0.

    所以x1＋x2＝，x1x2＝.

    ＝x1x2＋y1y2＝(1＋k2)x1x2＋k(x1＋x2)＋1＝＋8.

    由题设可得＋8＝12，解得k＝1，

    所以直线l的方程为y＝x＋1.

    故圆心C在直线l上，所以|MN|＝2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】有两枚均匀的硬币和一枚不均匀的硬币，其中不均匀的硬币抛掷后出现正面的概率为，小华先抛掷这三枚硬币，然后小红再抛掷这三枚硬币.

    （1）求小华抛得一个正面两个反面且小红抛得两个正面一个反面的概率；

    （2）若用表示小华抛得正面的个数，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知．

    （1）当时，求的值域；

    （2）若b为正实数，的最大值为M，最小值为m，且满足，求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示，在正方体中，设BC的中点为M，GH的中点为N。

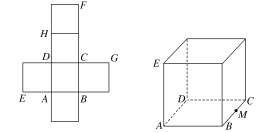
    (1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；

    (2)证明：直线MN∥平面BDH；

    (3)过点M，N，H的平面将正方体分割为两部分，求这两部分的体积比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为为参数），以该直角坐标系的原点为极点, 轴的正半轴为极轴的极坐标系下，曲线的方程为.

    （1）求曲线的普通方程和曲线的直角坐标方程；

    （2）设曲线和曲线的交点为、，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地有10个著名景点，其中8 个为日游景点，2个为夜游景点．某旅行团要从这10个景点中选5个作为二日游的旅游地．行程安排为第一天上午、下午、晚上各一个景点，第二天上午、下午各一个景点．

    （1）甲、乙两个日游景点至少选1个的不同排法有多少种？

    （2）甲、乙两日游景点在同一天游玩的不同排法有多少种？

    （3）甲、乙两日游景点不同时被选，共有多少种不同排法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求和函数的极值；

    （2）若关于的方程有3个不同实根，求实数的取值范围；

    （3）直线为曲线的切线，且经过原点，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有一个食品商店为了调查气温对热饮销售的影响，经过调查得到关于卖出的热饮杯数与当天气温的数据如下表，绘出散点图如下．通过计算，可以得到对应的回归方程＝－2.352x＋147.767，根据以上信息，判断下列结论中正确的是( )

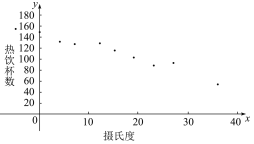
    摄氏温度

    －5

    0

    4

    7

    12

    15

    19

    23

    27

    31

    36

    热饮杯数

    156

    150

    132

    128

    130

    116

    104

    89

    93

    76

    54

    A.气温与热饮的销售杯数之间成正相关

    B．当天气温为2℃时，这天大约可以卖出143杯热饮

    C．当天气温为10℃时，这天恰卖出124杯热饮

    D．由于x＝0时，的值与调查数据不符，故气温与卖出热饮杯数不存在线性相关性

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某省两相近重要城市之间人员交流频繁，为了缓解交通压力，特修一条专用铁路，用一列火车作为交通车，已知该车每次拖4节车厢，一日能来回16次，如果每次拖7节车厢，则每日能来回10次．

    （1）若每日来回的次数是车头每次拖挂车厢节数的一次函数，求此一次函数解析式：

    （2）在（1）的条件下，每节车厢能载乘客110人．问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。

    查看答案和解析>>

    同步练习册答案