
【题目】已知函数![]() .
.
(1)求![]() 和函数
和函数![]() 的极值;
的极值;
(2)若关于![]() 的方程
的方程![]() 有3个不同实根,求实数
有3个不同实根,求实数![]() 的取值范围;
的取值范围;
(3)直线![]() 为曲线
为曲线![]() 的切线,且经过原点,求直线
的切线,且经过原点,求直线![]() 的方程.
的方程.
【答案】(1)当![]() ,
, ![]() 取极大值0,当
取极大值0,当![]() 时,取极小值
时,取极小值![]() (2)
(2)![]() (3)直线
(3)直线![]() 的方程
的方程![]() 或
或![]() .
.
【解析】试题分析:(1)求导![]() ,赋值,解得
,赋值,解得![]() ,可得
,可得![]() 进而得
进而得![]() 的极值.
的极值.
(2)若关于![]() 的方程
的方程![]() 有3个不同实根转化为
有3个不同实根转化为![]() 与
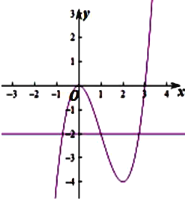
与![]() 有三个不同的交点,结合函数图象可知,所以
有三个不同的交点,结合函数图象可知,所以![]() .
.
(3)未知切点,因此设切点为![]() ,写出切线方程为
,写出切线方程为![]() ,由切线过
,由切线过![]() ,求得
,求得![]() ,即得切线方程.
,即得切线方程.
试题解析:(1)解:由![]() ,求导
,求导![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴![]() ,
, ![]() ,
,
令![]() ,解得
,解得![]() ,
, ![]() ,由
,由![]() 变化,
变化,

则当![]() ,
, ![]() 取极大值0,当
取极大值0,当![]() 时,取极小值
时,取极小值![]()
(2)解:由题意可知: ![]() 与
与![]() 有三个不同的交点,由函数图象可知,所以
有三个不同的交点,由函数图象可知,所以![]() .
.
(3)解:设切点![]() ,切线斜率
,切线斜率![]() ,则切线方程
,则切线方程![]() ,由切线过
,由切线过![]() ,则
,则![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() ,切线
,切线![]() ,切线方程
,切线方程![]() ,
,
当![]() ,切点
,切点![]() ,切线
,切线![]() ,切线方程
,切线方程![]() ,直线
,直线![]() 的方程
的方程![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() 为参数), 以坐标原点
为参数), 以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 分别交
分别交![]() 于
于![]() 两点, 求
两点, 求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1,a14=b4.
(1)求{an}的通项公式;
(2)设cn=an+bn,求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
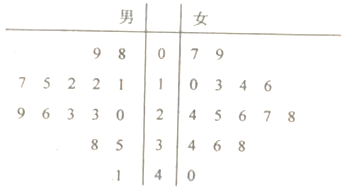
【题目】葫芦岛市某工厂党委为了研究手机对年轻职工工作和生活的影响情况做了一项调查:在厂内用简单随机抽样方法抽取了30名25岁至35岁的职工,对其“每十天累计看手机时间”(单位:小时)进行调查,得到茎叶图如下.所抽取的男职工“每十天累计看手机时间”的平均值和所抽取的女生 “每十天累计看手机时间”的中位数分别是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
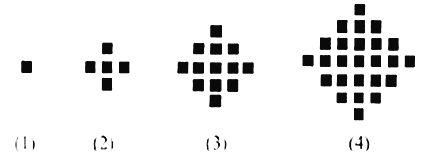
【题目】某少数民族的刺绣有着悠久的历史,如图(1),(2),(3),(4)为最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第![]() 个图形包含
个图形包含![]() 个小正方形.
个小正方形.
(1)求出![]() 的值;
的值;
(2)利用合情推理的“归纳推理思想”,归纳出![]() 与
与![]() 之间的关系式,并根据你得到的关系式求出
之间的关系式,并根据你得到的关系式求出![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):
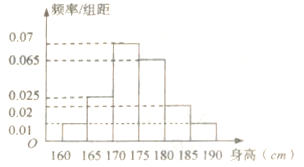
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acos θ(a>0),过点P(-2,-4)的直线l: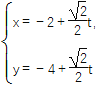 (t为参数)与曲线C相交于M,N两点.
(t为参数)与曲线C相交于M,N两点.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 也是抛物线
也是抛物线![]() 的焦点,点M为
的焦点,点M为![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)平面上的点N满足![]() ,直线
,直线![]() ,且与
,且与![]() 交于A,B两点,若
交于A,B两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com