
分析 (1)求出导函数,令导函数小于0的解集为单调递减区间;得到-1,$\frac{1}{3}$ 是导函数的两个零点,代入求出a的值;
(2)分别求出A,B的点坐标,求出直线AB的斜率,再根据AC⊥AB得到直线AC的斜率,求出直线AC的方程,与函数f(x)构成方程组,求出点C的坐标,继而求出三角形的面积;
(3)f(x)=(x-1)(ax2+2x+1),f(x)=0有三个根,x1,x2,x3,其中一个根为1,分别讨论,根据函数的性质求出a的取值范围即可.
解答 解:(1)f′(x)=3ax2+2(2-a)x-1
∵f(x)的单调递减区间为(-1,$\frac{1}{3}$),
∴-1,$\frac{1}{3}$是f′(x)=3ax2+2(2-a)x-1=0的两个根,
∴-1×$\frac{1}{3}$=-$\frac{1}{3a}$,
所以a=1,
(2)由(1)得f(x)=x3+x2-x-1,
且f(x)在(-∞,-1)和($\frac{1}{3}$,+∞)单调递增,在(-1,$\frac{1}{3}$)单调递减,
∴当x=-1时,函数f(x)有极大值,且f(-1)=-1+1+1-1=0,
∴A(-1,0),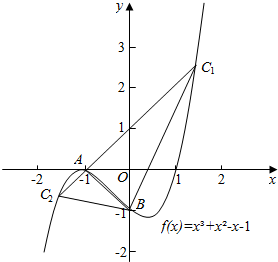
当x=0时,f(0)=-1,
∴B(0,-1),
画出函数f(x)的图象,如图所示,
假设存在这样的点C,
∵A(-1,0),B(0,-1),
∴kAB=-1,
∵AC⊥AB,
∴kAC=1,
∴过点A的直线方程为y=x+1,
∴$\left\{\begin{array}{l}{y=x+1}\\{y={x}^{3}+{x}^{2}-x-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\sqrt{2}}\\{y=\sqrt{2}+1}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-\sqrt{2}}\\{y=-\sqrt{2}+1}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$,
∴C点坐标为($\sqrt{2}$,$\sqrt{2}$+1)或(-$\sqrt{2}$,1-$\sqrt{2}$)
∴|AB|=$\sqrt{2}$,|AC|=2+$\sqrt{2}$,|AC2|=$\sqrt{6}$,
∴S△ABC=$\frac{1}{2}$|AB|•|AC|=$\frac{1}{2}$×$\sqrt{2}$×(2+$\sqrt{2}$)=$\sqrt{2}$+1,
或S△ABC=$\frac{1}{2}$|AB|•|AC|=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{6}$=$\sqrt{3}$
(3)f(x)=ax3+(2-a)x2-x-1=a(x3-x2)+(2x2-x-1)=ax2(x-1)+(x-1)(2x+1)=(x-1)(ax2+2x+1),
∵f(x)=0有三个根,x1,x2,x3,
∴ax2+2x+1=0有两根,
∴△=4-4a≥0,解得a≤1,
①若x1=1,则$\frac{1}{2}$≤x2≤2,
即ax2+2x+1=0在[$\frac{1}{2}$,2]上有解,
∴a=-$\frac{1}{{x}^{2}}$-$\frac{2}{x}$=-($\frac{1}{x}$+1)2+1,x∈[$\frac{1}{2}$,2],
∵$\frac{1}{2}$≤x≤2,
∴$\frac{1}{2}$≤$\frac{1}{x}$≤2,
∴-8≤-($\frac{1}{x}$+1)2+1≤-$\frac{5}{4}$,
即-8≤a≤-$\frac{5}{4}$,
②若x2=1,则$\frac{1}{2}$≤x1≤2,同理可得-8≤a≤-$\frac{5}{4}$,
③若x3=1,则x1,x2是方程ax2+2x+1=0的两根,
设$\frac{{x}_{1}}{{x}_{2}}$=k∈[$\frac{1}{2}$,2],则x1=kx2,
∵x1+x2=-$\frac{2}{a}$,x1x2=$\frac{1}{a}$,
∴$\left\{\begin{array}{l}{(k+1){x}_{2}=-\frac{2}{a}}\\{k{{x}_{2}}^{2}=\frac{1}{a}}\end{array}\right.$,
消去x2得$\frac{4}{a}$=$\frac{(k+1)^{2}}{k}$=$\frac{{k}^{2}+2k+1}{k}$=k+$\frac{1}{k}$+2,
设y=k+$\frac{1}{k}$+2,
则y在[$\frac{1}{2}$,1)上单调递减,在(1,2]上单调递增,
当k=1时,有最小值,即为1+1+2=4,
当k=2或k=$\frac{1}{2}$时,有最大值,最大值为2+$\frac{1}{2}$+2=$\frac{9}{2}$,
∴4≤$\frac{4}{a}$≤$\frac{9}{2}$,
∴$\frac{8}{9}$≤a≤1,
综上所述,a的取值范围为[-8,-$\frac{5}{4}$]∪[$\frac{8}{9}$,1]
点评 本题考查利用导函数求函数的单调区间,函数的极值,直线与直线垂直,直线方程,三角形的面积,方程组的解,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
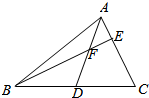 △ABC中,D为BC的中点,E为AC边上靠近点A的一个三等分点,AD与BE交于点F,求:
△ABC中,D为BC的中点,E为AC边上靠近点A的一个三等分点,AD与BE交于点F,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com