
已知函数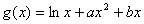 ,,函数
,,函数 的图象在点
的图象在点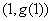 处的切线平行于
处的切线平行于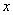 轴.
轴.
(1)确定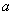 与
与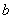 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意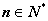 ,都有
,都有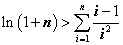 成立。
成立。
(1)依题意得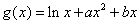 ,则
,则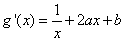
由函数 的图象在点
的图象在点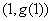 处的切线平行于
处的切线平行于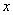 轴得:
轴得: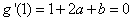
 ∴
∴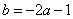
(2)由(1)得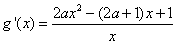
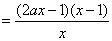 -
-
∵函数 的定义域为
的定义域为
∴①当 时,
时, 在
在 上恒成立,
上恒成立,
由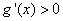 得
得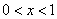 ,由
,由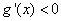 得
得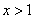 ,
,
即函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在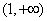 单调递减;-
单调递减;-
当 时,令
时,令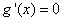 得
得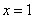 或
或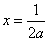 ,
,
②若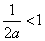 ,即
,即 时,由
时,由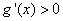 得
得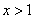 或
或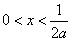 ,由
,由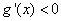 得
得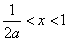 ,
,
即函数 在
在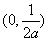 ,
,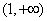 上单调递增,在
上单调递增,在 单调递减;
单调递减;
③若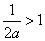 ,即
,即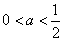 时,由
时,由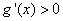 得
得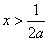 或
或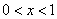 ,由
,由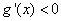 得
得 ,
,
即函数 在
在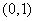 ,
,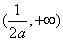 上单调递增,在
上单调递增,在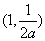 单调递减;-
单调递减;-
④若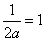 ,即
,即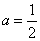 时,在
时,在 上恒有
上恒有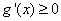 ,
,
即函数 在
在 上单调递增,
上单调递增,
综上得:当 时,函数
时,函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在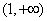 单调递减;
单调递减;
当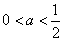 时,函数
时,函数 在
在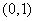 单调递增,在
单调递增,在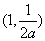 单调递减;在
单调递减;在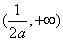 上单调递增;
上单调递增;
当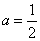 时,函数
时,函数 在
在 上单调递增,
上单调递增,
当 时,函数
时,函数 在
在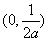 上单调递增,在
上单调递增,在 单调递减;在
单调递减;在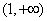 上单调递增.
上单调递增.
(3)证法一:由(2)知当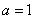 时,函数
时,函数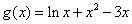 在
在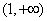 单调递增,
单调递增,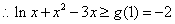 ,即
,即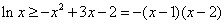 ,
,
令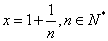 ,则
,则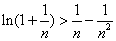 ,
,
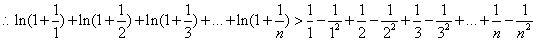
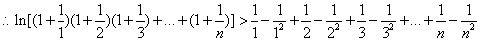
即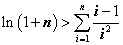
【证法二:构造数列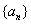 ,使其前
,使其前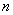 项和
项和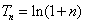 ,
,
则当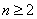 时,
时,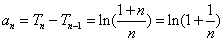 ,
,
显然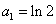 也满足该式,
也满足该式,
故只需证
令 ,即证
,即证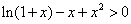 ,记
,记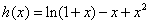 ,
,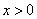
则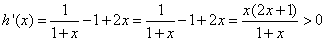 ,
,
 在
在 上单调递增,故
上单调递增,故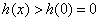 ,
,
∴ 成立,
成立,
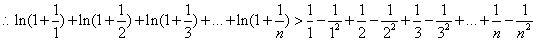
即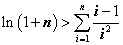 .
.
【证法三:令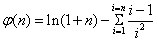 ,
,
则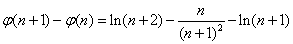
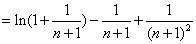 ----10分
----10分
令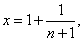 则
则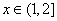 ,
,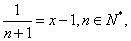
记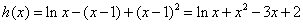 -
-
∵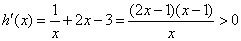 ∴函数
∴函数 在
在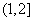 单调递增,
单调递增,
又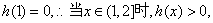 即
即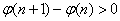 ,
,
∴数列 单调递增,又
单调递增,又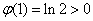 ,∴
,∴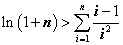


科目:高中数学 来源: 题型:
已知函数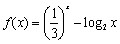 ,正实数
,正实数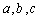 是公差为正数的等差数列,且满足
是公差为正数的等差数列,且满足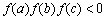 .若实数
.若实数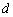 是方程
是方程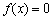 的一个解,那么下列四个判断:①
的一个解,那么下列四个判断:①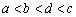 ;②
;②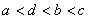 ;③
;③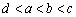 ;④
;④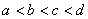 中有可能成立的个数为 ( )
中有可能成立的个数为 ( )
A.①② B.②③ C.③④ D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数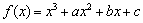 ,若
,若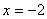 时,
时,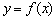 有极值.
有极值.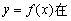
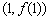 处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为
处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为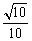 .
.
(1)求函数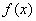 的解析式。
的解析式。
(2)若函数 的图像与直线
的图像与直线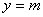 有三个不同的公共点,求实数
有三个不同的公共点,求实数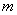 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com