
(1)求证:y=f(x)与y=g(x)的图象交于不同的两点A,B;
(2)求证:方程f(x)-g(x)=0的两根都小于2;
(3)求有向线段AB在x轴上的射影A1B1的长度的变化范围.
解析:∵a>b>c,a+b+c=0,
∴a>0,c<0.
(1)证明:由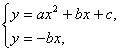 消去y,得
消去y,得
ax2+2bx+c=0.①
∴两图象交于不同的两点A,B?方程①有两个不同实数解.
∵a>0,c<0,
∴Δ>0,∴方程①有两个不同的实根.
(2)证明:令F(x)=ax2+2bx+c.
∴方程f(x)-g(x)=0的两根都小于2?y=F(x)的图象与x轴的交点在点(2,0)的左侧.
∵a>0,
∴只需证对称轴x=-![]() <2,且F(2)>0.
<2,且F(2)>0.
而a>b>c,a+b+c=0,
∴a+2b>0,∴-![]() <
<![]() <2.
<2.
又F(2)=4a+4b+c=3(a+b)=3(-c)>0,
故命题(2)得证.
(3)设A(x1,y1),B(x2,y2),
则A1(x1,0),B1(x2,0).
∴|A1B1|=|x1-x2|
=![]() .
.
∵a>b>c,a+b+c=0,
∴2a+c>0,且a+2c<0.
∴-2<![]() <-
<-![]() ,
,
∴|A1B1|∈(![]() ).
).


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| x |
| 1 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| bx-1 | a2x+2b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| bx-1 | a2x+2b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com