
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,若存在
,若存在![]() ,使得不等式
,使得不等式![]() 成立,求m的取值范围.
成立,求m的取值范围.
【答案】(1)当![]() 时,函数在
时,函数在![]() 上单调递增;当
上单调递增;当![]() 时,函数在
时,函数在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)
上单调递减;(2)![]()
【解析】
(1)求得函数的导函数为![]() ,再
,再![]() 和
和![]() 两种情况讨论可得;
两种情况讨论可得;
(2)若存在![]() ,使得不等式
,使得不等式![]() 成立,即存在
成立,即存在![]() ,使得不等式
,使得不等式![]() 成立,令
成立,令![]() ,
,![]() ,则
,则![]() ,求出函数的导数,说明其单调性及最小值,即可求出参数的取值范围;
,求出函数的导数,说明其单调性及最小值,即可求出参数的取值范围;
解:(1)函数![]() 的定义域为
的定义域为![]() ,
,
且![]()
当![]() ,即
,即![]() 时,
时,![]() 恒成立,故函数在
恒成立,故函数在![]() 上单调递增;
上单调递增;
当![]() ,即
,即![]() 时,令
时,令![]() ,解得
,解得![]() ,故函数在
,故函数在![]() 上单调递增;
上单调递增;
令![]() ,解得
,解得![]() ,故函数在
,故函数在![]() 上单调递减;
上单调递减;
综上所述,当![]() 时,函数在
时,函数在![]() 上单调递增;当
上单调递增;当![]() 时,函数在
时,函数在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)若存在![]() ,使得不等式
,使得不等式![]() 成立,即存在
成立,即存在![]() ,使得不等式
,使得不等式![]() 成立,
成立,
令![]() ,
,![]() ,则
,则![]() ,
,
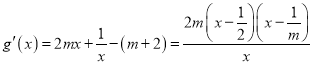
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上恒成立,故函数
上恒成立,故函数![]() 在
在![]() 上单调递增,
上单调递增,![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,则
上单调递增,则![]()
令![]() ,
,![]() ,
,![]() 恒成立,即函数
恒成立,即函数![]() ,在
,在![]() 上单调递减,又
上单调递减,又![]() 故
故![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,故
,故![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上恒成立,故函数
上恒成立,故函数![]() 在
在![]() 上单调递减,
上单调递减,![]() ,不符题意,舍去;
,不符题意,舍去;
综上可得![]()


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水.已知该厂生活用水为每小时10吨,生产用水量![]() (吨)与时间
(吨)与时间![]() (单位:小时,且规定早上6时
(单位:小时,且规定早上6时![]() )的函数关系式为:
)的函数关系式为:![]() ,水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管.
,水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管.
(1)若进水量选择为![]() 级,水塔中剩余水量为
级,水塔中剩余水量为![]() 吨,试写出
吨,试写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如何选择进水量,既能始终保证该厂的用水(水塔中水不空)又不会使水溢出?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,![]() 是等边三角形,D.E分别是BC.AC上两点,且
是等边三角形,D.E分别是BC.AC上两点,且![]() ,
,![]() 与AD交于点H,链接CH.
与AD交于点H,链接CH.
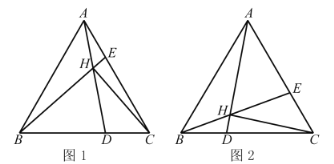
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)如图2,当![]() 时,
时,![]() __________;
__________;![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某健身馆为响应十九届四中全会提出的“聚焦增强人民体质,健全促进全民健身制度性举措”,提高广大市民对全民健身运动的参与程度,推出了健身促销活动,收费标准如下:健身时间不超过1小时免费,超过1小时的部分每小时收费标准为20元(不足l小时的部分按1小时计算).现有甲、乙两人各自独立地来该健身馆健身,设甲、乙健身时间不超过1小时的概率分别为![]() ,
,![]() ,健身时间1小时以上且不超过2小时的概率分别为
,健身时间1小时以上且不超过2小时的概率分别为![]() ,
,![]() ,且两人健身时间都不会超过3小时.
,且两人健身时间都不会超过3小时.
(1)设甲、乙两人所付的健身费用之和为随机变量![]() (单位:元),求
(单位:元),求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)此促销活动推出后,健身馆预计每天约有300人来参与健身活动,以这两人健身费用之和的数学期望为依据,预测此次促销活动后健身馆每天的营业额.
查看答案和解析>>
科目:高中数学 来源: 题型:
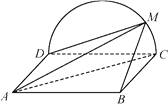
【题目】如图,边长为2的正方形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求面
体积最大时,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一些选手参加数学竞赛,其中有些选手互相认识,有些选手互相不认识,而任何两个不相识的选手都恰有两个共同的熟人.若![]() 与
与![]() 认识,但没有共同的熟人,求证:
认识,但没有共同的熟人,求证:![]() 、
、![]() 认识的熟人一样多.
认识的熟人一样多.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com