
【题目】设数列{an}的各项均为正数.若对任意的n∈N* , 存在k∈N* , 使得an+k2=anan+2k成立,则称数列{an}为“Jk型”数列.
(1)若数列{an}是“J2型”数列,且a2=8,a8=1,求a2n;
(2)若数列{an}既是“J3型”数列,又是“J4型”数列,证明:数列{an}是等比数列.
【答案】
(1)解:∵数列{an}是“J2”型数列,
∴ ![]() =anan+4
=anan+4
∴数列{an}的奇数项、偶数项分别组成等比数列
设偶数项组成的等比数列的公比为q,
∵a2=8,a8=1,∴ ![]() ,∴q=
,∴q= ![]()
∴a2n=8× ![]() =24﹣n;
=24﹣n;
(2)解:由题设知,当n≥8时,an﹣6,an﹣3,an,an+3,an+6成等比数列;an﹣6,an﹣2,an+2,an+6也成等比数列.
从而当n≥8时,an2=an﹣3an+3=an﹣6an+6,(*)且an﹣6an+6=an﹣2an+2.
所以当n≥8时,an2=an﹣2an+2,即 ![]()
于是当n≥9时,an﹣3,an﹣1,an+1,an+3成等比数列,从而an﹣3an+3=an﹣1an+1,故由(*)式知an2=an﹣1an+1,
即 ![]() .
.
当n≥9时,设 ![]() ,当2≤m≤9时,m+6≥8,从而由(*)式知am+62=amam+12,
,当2≤m≤9时,m+6≥8,从而由(*)式知am+62=amam+12,
故am+72=am+1am+13,从而 ![]() ,
,
于是 ![]() .
.
因此 ![]() 对任意n≥2都成立.
对任意n≥2都成立.
因为 ![]() ,所以
,所以 ![]() ,
,
于是 ![]() .
.
故数列{an}为等比数列.
【解析】(1)利用数列{an}是“J2”型数列,可得数列{an}的奇数项、偶数项分别组成等比数列,根据a2=8,a8=1,求出数列的公比,即可得到通项;(2)由题设知,当n≥8时,an﹣6 , an﹣3 , an , an+3 , an+6成等比数列;an﹣6 , an﹣2 , an+2 , an+6也成等比数列,可得 ![]() ,进而可得
,进而可得 ![]() ,
, ![]() 对任意n≥2都成立,由此可得数列{an}为等比数列.
对任意n≥2都成立,由此可得数列{an}为等比数列.
【考点精析】本题主要考查了等比关系的确定和数列的通项公式的相关知识点,需要掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线方程为![]() ,问:是否存在过点M(1,1)的直线l,使得直线与双曲线交于P,Q两点,且M是线段PQ的中点?如果存在,求出直线的方程,如果不存在,请说明理由.
,问:是否存在过点M(1,1)的直线l,使得直线与双曲线交于P,Q两点,且M是线段PQ的中点?如果存在,求出直线的方程,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某广场中间有一块边长为2百米的菱形状绿化区ABCD,其中BMN是半径为1百米的扇形,∠ABC= ![]() .管理部门欲在该地从M到D修建小路:在
.管理部门欲在该地从M到D修建小路:在 ![]() 上选一点P(异于M,N两点),过点P修建与BC平行的小路PQ.
上选一点P(异于M,N两点),过点P修建与BC平行的小路PQ. 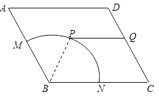
(1)若∠PBC= ![]() ,求PQ的长度;
,求PQ的长度;
(2)当点P选择在何处时,才能使得修建的小路 ![]() 与PQ及QD的总长最小?并说明理由.
与PQ及QD的总长最小?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() 是非零不共线的向量,设
是非零不共线的向量,设 ![]() =
= ![]()
![]() +
+ ![]()
![]() ,定义点集M={K|
,定义点集M={K| ![]() =
= ![]() },当K1 , K2∈M时,若对于任意的r≥2,不等式|
},当K1 , K2∈M时,若对于任意的r≥2,不等式| ![]() |≤c|
|≤c| ![]() |恒成立,则实数c的最小值为 .
|恒成立,则实数c的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +
+ ![]() =1,圆C2:x2+y2=t经过椭圆C1的焦点.
=1,圆C2:x2+y2=t经过椭圆C1的焦点.
(1)设P为椭圆上任意一点,过点P作圆C2的切线,切点为Q,求△POQ面积的取值范围,其中O为坐标原点;
(2)过点M(﹣1,0)的直线l与曲线C1 , C2自上而下依次交于点A,B,C,D,若|AB|=|CD|,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 在其定义域内存在
在其定义域内存在![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 为“可分拆函数”.
为“可分拆函数”.
(1)试判断函数![]() 是否为“可分拆函数”?并说明你的理由;
是否为“可分拆函数”?并说明你的理由;
(2)设函数![]() 为“可分拆函数”,求实数
为“可分拆函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com