
【题目】函数![]() 的零点个数为_____.
的零点个数为_____.
【答案】2
【解析】
先利用导数判断函数的单调性,然后求出f(x)的极大值与极小值,再说明f(x)有几个零点.
对函数f(x)进行求导:f'(x)=3x2+6x﹣9
令f'(x)=0,则(x+3)(x﹣1)=0x1=1,x2=﹣3
当x∈(﹣∞,﹣3)时,f'(x)>0,f(x)在(﹣∞,-3)上单调递增;
当x∈(﹣3,1)时,f'(x)<0,f(x)在(-3,1)上单调递减;
当x∈(1,+∞)时,f'(x)>0,f(x)在(1,+∞)上单调递增;
当x=﹣3时,函数f(x)![]() = f(-3)=32;
= f(-3)=32;
当x=1时,函数f(x)![]() = f(1)=0,
= f(1)=0,
根据零点存在定理,所以f(x)有2个零点.
故答案为;2


科目:高中数学 来源: 题型:
【题目】如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC. 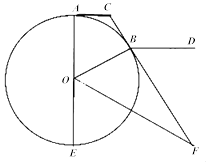
(1)证明:OB2=BCBF;
(2)证明:∠DBF=∠AOB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C,D为平面四边形ABCD的四个内角. 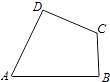
(1)证明:tan ![]() =
= ![]() ;
;
(2)若A+C=180°,AB=6,BC=3,CD=4,AD=5,求tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:y2=2x﹣4.
(1)求曲线C在点A(3, ![]() )处的切线方程;
)处的切线方程;
(2)过原点O作直线l与曲线C交于A,B两不同点,求线段AB的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:x2=y,圆C2:x2+(y﹣4)2=1的圆心为点M
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}中的项都满足a2n﹣1=a2n<a2n+1(n∈N*),则称{an}为“阶梯数列”.
(1)设数列{bn}是“阶梯数列”,且b1=1,b2n+1=9b2n﹣1(n∈N*),求b2016;
(2)设数列{cn}是“阶梯数列”,其前n项和为Sn , 求证:{Sn}中存在连续三项成等差数列,但不存在连续四项成等差数列;
(3)设数列{dn}是“阶梯数列”,且d1=1,d2n+1=d2n﹣1+2(n∈N*),记数列{ ![]() }的前n项和为Tn , 问是否存在实数t,使得(t﹣Tn)(t+
}的前n项和为Tn , 问是否存在实数t,使得(t﹣Tn)(t+ ![]() )<0对任意的n∈N*恒成立?若存在,请求出实数t的取值范围;若不存在,请说明理由.
)<0对任意的n∈N*恒成立?若存在,请求出实数t的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的各项均为正数.若对任意的n∈N* , 存在k∈N* , 使得an+k2=anan+2k成立,则称数列{an}为“Jk型”数列.
(1)若数列{an}是“J2型”数列,且a2=8,a8=1,求a2n;
(2)若数列{an}既是“J3型”数列,又是“J4型”数列,证明:数列{an}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过![]() 米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
(1)把房屋总造价![]() 表示成
表示成![]() 的函数,并写出该函数的定义域.
的函数,并写出该函数的定义域.
(2)当侧面的长度为多少时,总造价最底?最低总造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com